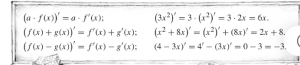Argumentavimo būdai mokyklinėje matematikoje

Mokyklinė matematika Add comments

Grd 182022

Santrauka. Skirtingai nuo gamtos mokslų, kuriuose eksperimentas yra pagrindinis argumentavimo būdas, matematikoje argumentuojama pagrindžiant ar įrodant. Matematinio argumentavimo specifiką sudaro matematinio objekto prigimtis ir matematinės apibrėžties savybės. Įrodymo vaidmuo mokyklinėje matematikoje iliustruojamas kvadratinės šaknies ir jos savybių nagrinėjimo pavyzdžiais. Šis pavyzdys apibendrinamas apžvelgiant logikos naudojimą matematikos vadovėliuose. Matematinio objekto apibrėžties ypatumai aptariami nagrinėjant funkcijos, kintamojo ir reiškinio sąvokų naudojimą matematikos vadovėliuose. Tekstas parašytas matematikos mokytojams skaityto pranešimo pagrindu. Jo metu buvo atlikta apklausa, kuri komentuojama teksto gale.

Įvadas

Matematikos dalykas skiriasi nuo kitų mokomųjų dalykų savo objektu ir argumentavimo būdais. Pavyzdžiui, gamtos moksluose nagrinėjami realūs daiktai ir jų savybės. Šiuose moksluose pagrindinis argumentavimo būdas yra eksperimentas. Jo pagrindu atsiranda spėjimai, tvirtinamos arba paneigiamos gamtos mokslų teorijos. Matematika gamtos moksluose yra svarbi, bet tik kaip pagalbinė priemonė. Matematinė priemonė keičiama priklausomai nuo jos naudingumo paaiškinti realius reiškinius. Matematika laikoma tarsi receptų knyga, gamtos kalba ir t.t. Tokią matematiką tiksliau būtų vadinti taikomąja matematika.

Kam apskritai matematika reikalinga mokykloje visiems, jei ne kaip taikomoji matematika? Siūlau tris lygiavertes priežastis. Pirma, matematika yra taikomosios matematikos šaltinis. Pažįstant tokį šaltinį, galima nujausti įvairiausių problemų sprendimo galimybes. Antra, matematika būdama reikšminga žmonijos kultūros dalimi yra kiekvieno žmogaus būtinąja išsilavinimo dalimi. Trečia, matematika būdama mąstymo srities menu suteikia žmogui galimybę praturtėti dar vienos meno rūšies supratimu. Šių priežasčių įgyvendinamas apsunkinamas, kai matematikos mokoma tik ,,gyvenimui“ ir profesijai.

Pagal [13], argumentavimas matematikos pamokoje yra mokinių ir mokytojų vykdoma paieška tokių teiginių, kuriais galima pademonstruoti ar paaiškinti jų matematinės veiklos rezultatus. Matematinės veiklos rezultatai gali būti bendri teiginiai apie matematinių objektų klases, jų savybes arba matematinės užduoties sprendimo rezultatas. Šia prasme, matematinio argumentavimo rezultatas gali būti teiginio įrodymas ar paaiškinimas, kaip ir kodėl mokinys ar mokytojas suformulavo tam tikrą spėjimą, kaip samprotavo spręsdami užduotį, arba paprasčiausia skaičiavimų seka, atvedanti prie konkretaus skaičiaus.

Matematinis objektas

Kas yra matematinis objektas ir kodėl apskritai šis klausimas turi prasmę? Taip, turi prasmę, jei norime atsakyti į klausimą: Kas yra matematika? Atsakymų variantų į šį klausimą yra daugybė. Mums prasmę šiam klausimui suteikia noras suprasti, kuo mokyklinės matematikos dalykas skiriasi nuo kitų mokomųjų dalykų ir kodėl tiek daug mokinių turi sunkumų mokydamiesi matematikos?

Šią vasarą vykusiame Tarptautiniame matematikų organizacijos kongrese šiuos klausimus formulavo ir atsakymus į juos pasiūlė matematikos mokymo tyrėja Anna Sfard [12]. Išsakysiu keletą jos minčių.

Jei matematiniais objektais, tokiais kaip skaičiai, funkcijos, yra tik simboliai kuriuos rašome, tai kaip paaiškinti reiškinių lygybės prasmę

$x^2-1 = (x-1)(x+1)$ ?

Iš pažiūros abiejose lygybės pusėse užrašyti simboliai yra skirtingi. Kodėl tarp jų galima dėti lygybės ženklą? Kas yra bendro abiejose lygybės pusėse?

Matematikai sako, kad lygiais yra skaičiai, kuriuos gauname abiejose lygybės pusėse vietoje $x$ įstatę bet kurį skaičių, arba, kitaip tariant, lygiomis yra funkcijos apibrėžtos reiškiniais esančiais abiejose lygybės pusėse. Taigi, nors reiškiniai sudarantys simbolines struktūras yra skirtingi, lygybę įprasmina skaičiais ir funkcijomis vadinami esiniai arba matematiniai objektai.

Šis pavyzdys paaiškina, kodėl daugeliui mokinių matematikos mokymasis panašus į mokymąsi manipuliuoti beprasmiais simboliais naudojant nesuprantamas taisykles. Už simbolių dažniausiai neįžvelgiami prasmę jiems suteikiantys matematiniai objektai.

Platonizmu vadinama matematikos filosofijos kryptis matematiniu objektu laiko nepriklausomai nuo žmogaus egzistuojantį esinį (abstrakciją), panašiai kaip uola egzistuojanti nepriklausomai nuo žmogaus valios. Matematiniu simboliu yra matematinio objekto materializacija, panašiai kaip avatara yra Dievo arba jo galios įsikūnijimas konkrečiu pavidalu. Tokia matematinio objekto samprata vadinama dualistine. Pagal šią dualistinę sampratą (formaliai) skiriame skaitmenį nuo skaičiaus. Daugelis matematikų laikosi platonizmo požiūrio į matematinius objektus. Tačiau daugumai kitų žmonių šis požiūris nepriimtinas.

Anna Sfard savo paskaitoje aiškina naują matematinio objekto sampratą. Pagal ją, matematinis objektas yra kalbos (diskurso) konstruktas, reiškiantis tik tai, kad mums patogu kalbėti apie įprastus procesus kaip apie daiktus. Toks proceso sudaiktinimas yra labai svarbus perteikti matematinę prasmę. Prie šios pastabos grįšime kalbėdami apie funkciją antroje paskaitos dalyje.

Neretai mokytojai intuityviai matematinius objektus įžvelgia už simbolių ir apie įvairias procedūras ir simbolius kalba taip lyg už jų matytų kažkokią prasmę. Be to, kalbėjimas apie daiktus-objektus komunikaciją padaro paprastesne. Tačiau naujokui toks kalbos konstruktas ir jo paskirtis nežinomi. Anna Sfard tai pavaizdavo dviem paveiksliukais.

Matematinė apibrėžtis

Matematinio objekto apibrėžtis skiriasi nuo ,,žodžio apibrėžties“ kasdieninėje kalboje. Leksikografijoje ,,žodžio apibrėžtis“ yra jo reikšmės aiškinimas. Matematikoje apibrėžtimi nusakomas sąvokos turinys ir sąvokos terminas, kurie besimokančiajam yra nauji. Kitaip tariant, apibrėžtimi tiksliai formuluojamos savybės, kuriomis vienareikšmiškai identifikuojamas matematinis objektas. Leksikografinė ,,apibrėžtis“ nusako kalboje priimtą žodžio reikšmę ir jo naudojimo praktiką, o matematinė apibrėžtis sukuria sąvoką ir jos naudojimo praktiką.

Būtinos matematinės apibrėžties savybės.

Hierarchinė struktūra: bet kuri nauja sąvoka turi būti kurios nors bendresnės sąvokos atskiru atveju.
Egzistavimas: reikalingas įrodymas, kad bent vienu atveju naujai apibrėžiama sąvoka egzistuoja.
Vienareikšmiškumas: apibrėžties savybės objektą nusako vienareikšmiškai.
Ekvivalentumas: jei yra du tos pačios sąvokos apibrėžimai, tai būtinas įrodymas, kad sąvoką apibrėžiančios savybės yra ekvivalenčios.

Pageidaujamos matematinės apibrėžties savybės.

Minimalumas: reikalingas tik minimalus savybių skaičius būtinas vienareikšmiškai nusakyti sąvoką.
Elegantiškumas: pageidautina tarp ekvivalenčių apibrėžčių pasirinkti tą, kuri lakoniškesnė arba kuri atrodo ,,gražiau“ (pvz. lygiašonis trikampis).

Mūsų matematikos vadovėliuose yra problemų su sąvokų apibrėžtimis, jos traktuojamos kaip kasdieninės kalbos žodžių apibrėžtys. Vėliau aptarsime šiuo požiūriu keletą svarbių sąvokų, būtent funkcijos, reiškinio ir kintamojo sąvokas. Kol kas pereisime prie įrodymo mokyklinėje matematikoje aptarimo.

Įrodymo vaidmuo mokyklinėje matematikoje

Kam reikalingas įrodymas mokykloje? Stereotipu yra požiūris, kad matematinis įrodymas yra tik teiginio teisingumo pagrindimas, turintis griežtą loginę struktūrą. Kadangi matematikos teiginiais niekas neabejoja, tai nėra reikalo vargti įrodinėjant mokykloje.

Matematikos mokymo tyrimai rodo, kad įrodymas mokykloje padeda:

atpažinti mąstymo klaidas (įrodymui reikalinga logika);
paaiškinti teiginį;
motyvuoti gilinimąsi į nuobodžius dalykus (pvz. trigonometrija);
atskleisti matematinio mąstymo specifiką (kritinio mąstymo kompetencija).

Toliau įrodymo galimybes iliustruosime kvadratinės šaknies sąvokos ir jos savybių aiškinimu.

Kvadratinė šaknis samprotaujant

Teigiamo skaičiaus $a$ kvadratinės šaknies sąvokos apibrėžimui parodysime, kad egzistuoja skaičius $x$ su savybe $x^2=a$ . Realiųjų skaičių aibę tapatiname su geometrine tiese. Todėl skaičių $x$ ieškosime skaičių tiesėje, t.y. ieškosime atkarpos, kurios ilgis $x$ su nurodyta savybe.

Kvadratinės šaknies egzistavimas

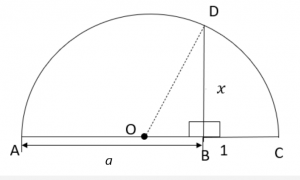
Tegul $a$ yra teigiamas realusis skaičius. Iš pradžių atidedame $a$ ilgio atkarpą AB. Po to pratęsiame 1 ilgio atkarpa BC. Randame atkarpos AC vidurį O ir brėžiame pusapskritimį su centru O ir spinduliu OC. Iš taško B brėžiame statmenį iki susikirtimo su pusapskritimiu taške D. Taškus O ir D sujungiame atkarpa. Sekantis eskizas brėžiamas atveju $a>1$ .

Naudodami Pitagoro teoremą trikampiui OBD, įsitikinsime, kad $x^2=|BD|^2=a$ . Atkarpos OB ilgis

$|OB|=|OC|-|BC|=\frac{a+1}{2}-1=\frac{a-1}{2}.$

Kadangi OD ir OC yra pusapskritimio spinduliai, tai

$|OD| = |OC|=\frac{a+1}{2}.$

Gauname

$|BD|^2=|OD|^2-|OB|^2=\Big (\frac{a+1}{2}\Big )^2-\Big (\frac{a-1}{2}\Big )^2=a.$

Reikia atlikti analogiškus samprotavimus ir brėžimą kai $0<a<1$ .

Kvadratinės šaknies vienatis

Tarkime, kad duotam skaičiui $a > 0$ , egzistuoja toks teigiamas skaičius $x$ , kad $x^2 = a$ . Įrodysime, kad toks $x$ yra vienintelis.

Tam pakanka įrodyti implikaciją:

Jei $x$ ir $y$ yra du teigiami realūs skaičiai ir $x^2 = y^2$ , tai $x=y$ . (1)

Implikacija yra teisinga, jei esant teisingai prielaidai būtinai teisinga išvada. Tegul teisinga prielaida, t.y. $x$ ir $y$ yra du teigiami realūs skaičiai ir $x^2 = y^2$ . Tada

$0 = x^2-y^2 =(x-y)(x+y).$ (2)

Įrodysime ir naudosime pagalbinį teiginį:

Lema. Bet kuriems realiesiems skaičiams $u$ ir $v$ , teisinga implikacija

jei $uv=0$ , tai $u=0$ arba $v=0$ . (3)

Įrodymas. Implikacija yra teisinga, jei esant teisingai prielaidai būtinai teisinga išvada. Tegul teisinga prielaida, t.y. $uv=0$ . Įrodysime, kad $u=0$ arba $v=0$ .

Teiginys $u=0$ yra teisingas arba klaidingas. Jei jis teisingas, tai lema įrodyta. Tarkime, kad jis klaidingas. Tada $u\not =0$ ir $\frac{1}{u}{\cdot}u=1$ remiantis prastinimo taisykle racionaliesiems skaičiams. Realiesiems skaičiams galime laikyti tai esant teisinga remiantis Mokyklinės matematikos fundamentaliąja prielaida [15; 265 pusl.]. Tada, abi lygybės $uv=0$ puses daugindami iš $\frac{1}{u}$ , gauname $1{\cdot}v=0$ . Todėl $v=0$ . Tai įrodo (3).

Dėl (2) lygybės ir lemos, turime $(x-y)(x+y)=0$ . Kadangi $x>0$ ir $y>0$ , $x+y>0$ . Todėl $x-y=0$ . Tai $x=y$ . (1) įrodyta.

Dabar galima korektiškai apibrėžti kvadratinės šaknies sąvoką.

Apibrėžtis. Neneigiamo realiojo skaičiaus $a$ kvadratine šaknimi vadinamas vienintelis neneigiamas skaičius $x$ , kurio kvadratas lygus $a$ . Skaičius $x$ žymimas simboliu $\sqrt{a}$ .

Įrodysime skaičių sandaugos kvadratinės šaknies savybę:

$\sqrt{a{\cdot}b} =\sqrt{a}\cdot\sqrt{b}$ visiems neneigiamiems realiesiems skaičiams a ir b. (4)

Remiantis kvadratinės šaknies vienaties savybe (1), pakanka įrodyti, kad

$\big (\sqrt{a{\cdot}b}\big )^2=\big (\sqrt{a}\cdot\sqrt{b}\big )^2.$

Kairioji šios lygybės pusė lygi $ab$ pagal kvadratinės šaknies apibrėžtį. Dešinioji šios lygybės pusė lygi

$\big(\sqrt{a}\cdot\sqrt{b}\big)\big(\sqrt{a}\cdot\sqrt{b}\big)=\big(\sqrt{a}\cdot\sqrt{a}\big)\big(\sqrt{b}\cdot\sqrt{b}\big )=ab.$

Tai įrodo (4).

Kvadratinė šaknis vadovėliuose

Kai kuriuose populiariuose vadovėliuose kvadratinė šaknis iš neneigiamo skaičiaus apibrėžiama nesirūpinant parodyti tokio skaičiaus egzistavimą ir jo vienatį. Tuo būdu praleidžiama proga dar kartą pasidalinti su mokiniais istorija apie nebendramates atkarpas arba $\sqrt{2}$ iracionalumą (žr [14; 52 pusl.]). Kai kuriuose vadovėliuose kvadratinės šaknies savybės tik patikrinamos konkretiems skaičiams. Toks argumentavimas būdingas ne matematikai, o gamtos mokslams.

Šioje vadovėlio ištraukoje ir puslapio apačioje rašoma: ,,Lygybė $\sqrt{a\pm b}=\sqrt{a}\pm\sqrt{b}$ yra teisinga tik tada, kai $a=b=0$ „. Jei šį teiginį įrodinėtume, tai aptiktume klaidą.

Kitoje prancūziško vadovėlio ištraukoje svarstomas tas pats sumos kvadratinės šaknies klausimas. Ištraukos idėjas galima suprasti nesuprantant kalbos.

Dviem būdais pagrindžiama, kad nelygybė $sqrt{a+b}\leq\sqrt{a}+\sqrt{b}$ teisinga visiems neneigiamiems $a$ ir $b$ .

Ištraukoje iš kito vadovėlio nepastebima, kad naudojama sandaugos kvadratinės šaknies savybė $\sqrt{ab}=\sqrt{a}\sqrt{b}$ . Nors pateikiami samprotavimai pretenduoja į ,,dedukcinį protavimą skatinančių metodų“ iliustravimą.

Dar viena šios vadovėlio ištraukos ypatybė – atsainus požiūris į kvantorius. Nelygybė tvirtinama galiojanti ,,visiems $a\geq 0$ ir $b\geq 0$ . Todėl samprotaujant prieštaros būdu svarbu atkreipti dėmesį į būtinumą keisti ,,visiems“ į ,,egzistuoja“. Šioje vietoje turėtų būti aiškinamas logikos faktas:

Neiginys [kiekvienam x teisinga S(x)] ekvivalentus teiginiui [egzistuoja x toks, kad ne S(x)],

čia S(x) – savybė, pavyzdžiui, nelygybė priklausanti nuo kurios nors aibės elementų x.

Logika dabartinėje mokyklinėje matematikoje

Visuomenėje paplitęs požiūris, kad matematika lavina loginį mąstymą. Ši matematikos savybė dažnai nurodoma kaip argumentas matematikos mokyti visus. Ar tikrai dabartinė mokyklinė matematika lavina loginį mąstymą?

Iki šiol, pagal matematikos mokymo programą, teiginių logika buvo atskiru moduliu. Tai reiškė, kad logikos žinios nebuvo privalomos. Dabartinėje atnaujintoje programoje 7 klasės geometrijos temoje yra šie sakiniai:

Ar to pakanka? Apžvelgtuose įrodymuose mes naudojame šiuos teiginių logikos elementus: teiginys, implikacija, ekvivalencija, kvantoriai, loginiai jungtukai. Jei mokyklinės matematikos turinyje mokinių gebėjimo įrodinėti lavinimui būtų skiriamas pagrindinis dėmesys, tai logikos elementai būtų formuluojami ir naudojami nuolat ir visose temose.

Net ir formuluojama kaip atskira tema logika vadovėlyje pateikiama nerūpestingai. Keletas logikos elementų pateikimo vadovėlyje pavyzdžių.

Šioje vadovėlio ištraukoje paaiškinama, kas yra teiginys ir pateikiama keletas teiginių pavyzdžių. Tarp pavyzdžių yra ir apibrėžčių. Tačiau matematinė apibrėžtis, skirtingai nuo žodžio reikšmės aiškinimo leksikografijoje, nėra teisinga arba klaidinga, t.y. nėra teiginys. Matematikoje dauguma sakinių ir formulių yra teiginiai. Pavyzdžiui, $2+2=5$ yra klaidingas teiginys. Be to, teiginys, kurio teisingumu įsitikinama samprotaujant, nebūtinai vadinamas teorema. Nors toks įspūdis gali susidaryti skaitant kitą vadovėlio ištrauką.

Ištraukoje matoma frazė ,,prijungiamasis sakinys“ yra kalbos gramatikos terminas. Jis reiškia sudėtinį sakinį, kurio dėmenys siejami prijungimo ryšiu (ką tai bereikštų). Šio vadovėlio kontekste turėtų būti kalbama apie teiginių logikos terminą ,,sąlyginį sakinį“ kitaip dar vadinamą ,,(materialiąją) implikaciją“. Kalbant apie implikaciją svarbu apibrėžti jo teisingumo ir klaidingumo reikšmes. Tai nėra priežastinius ryšius nurodantis teiginys.

Ne kiekvieno teiginio atvirkštinis teiginys privalo būti teisingas, kaip tvirtinama vadovėlio ištraukoje. Pavyzdžiui, teiginys ,,jei skaičius dalosi iš 4, tai jis dalosi iš 2“ yra teisingas. Šio teiginio atvirkštinis teiginys ,,jei skaičius dalosi iš 2, tai jis dalosi iš 4“ yra klaidingas. Kai naudojama implikacija ,,jei A, tai B“, svarbu žinoti, kad jos teisingumas nereiškia teiginio B teisingumą. Išvadą apie teiginio B teisingumą galima daryti tada, kai teisingi du teiginiai: teiginys ,,A“ ir implikacija ,,jei A, tai B“.

Kitoje ištraukoje paaiškinamas ,,prieštaros metodu“ vadinamas įrodymo būdas.

Tarkime, kad teoremos teiginio loginė forma yra ,,jei A, tai B“. Vadovėlyje būtina paaiškinti kaip atrodo implikacijai priešingas teiginys ,,ne [jei A, tai B]“. Būtent, jis turi loginę formą ,,A ir ne B“.

Įrodinėjimui naudojamas matematikos turinys turi tenkinti šiuos penkis principus:

Funkcija, kintamasis ir reiškinys

Šiame skyrelyje mūsų vadovėliuose naudojamos funkcijos sąvokos apibrėžtys aptariamos dviem aspektais: matematiniu ir pedagoginiu. Matematinis aspektas reiškia vadovėlio apibrėžties atitikimas anksčiau suformuluotiems matematinės apibrėžties reikalavimams. Tuo tarpu aptarimas pedagoginiu aspektu reiškia išryškinimą požymių parodančių vadovėlių autorių funkcijos supratimo lygį (procesas vs objektas). Kaip funkciją supranta vadovėlių autoriai, taip ji dažniausiai mokoma klasėje. Papildomą pagrindą funkcijos sampratos tarp mokytojų išsiaiškinimui suteikia mokytojų apklausos rezultatai ir jų statistinė analizė.

Pradžiai verta prisiminti seniau atliktos į ekonometrijos pirmą kursą įstojusių mokinių apklausos rezultatus. Vienas iš klausimų buvo skirtas funkcijos sampratai. Įdomu, ką apie funkciją pamena ką tik mokyklą baigę mokiniai. Apklausoje dalyvavo 51 studentas.

Buvusių mokinių atsakymuose apie funkciją labiausiai išsiskiria jų įvairovė. Matysime, kad toks rezultatas dėsningas. Vadovėliuose, apibrėžiant funkciją ir vėliau, apie ją pasakoma daug dalykų, netgi prieštaringų.

Kodėl apskritai turėtume rūpintis funkcijos samprata mokykloje? 20 a. pradžioje Felix Klein pasiūlė modernizuoti matematikos mokymą jos turinį grindžiant funkcijos sąvoką. Pagal F. Klein ir kitus, ,,funkcinis mąstymas“ turėtų apjungti atskiras mokyklinės matematikos turinio temas, tuo parodydamas matematikos vieningumą. Šią idėją bandė įgyvendinti tarpukario Lietuvos matematikos mokytojai. Pastaraisiais dešimtmečiais funkcijos sąvoka prarado savo svarbą, kartu su visa mokykline matematika. Funkcijos nagrinėjimą keičia algebrinio reiškinio nagrinėjimas, kai kurie veiksmai su funkcijomis įgyja naujas prasmes arba dingsta iš programos (atvirkštinė funkcija). Be to, skirtinguose vadovėliuose funkcija gali būti traktuojama skirtingai.

Funkcijos sąvokos apibrėžtis

Priminsime keletą funkcijos sąvokos evoliucijos momentų:

Newton‘as vienas pirmųjų funkciją siejo su nepriklausomu kintamuoju ir priklausomu kintamuoju.
Euler‘is (1748): Kintamojo dydžio funkcija yra analitinis reiškinys sudarytas iš kintamųjų dydžių, skaičių ir pastovių dydžių.
Dirichlet (1829): y yra kintamojo x funkcija, jei kiekvienai x reikšmei iš skaičių intervalo atitinka vienintelė y reikšmė.
Bourbaki (1939): Sąryšiu vadinamas aibių $X$ ir $Y$ Dekarto sandaugos $X\times Y$ poaibis, t.y. $X$ ir $Y$ elementų sutvarkytų porų aibė. Aibės $X$ elementas x yra funkciniame sąryšyje su aibės $Y$ elementu y, jei, duotam x, y yra vienintelis.

Bendra visoms apibrėžtims tai, kad funkcija išreiškia priklausomybę tarp objektų. Skiriasi objektų identifikavimo būdai (kintamasis, kintamasis dydis, aibės elementai) ir priklausomumo reiškimo būdai (analitinis reiškinys, taisyklė, sąryšis). Visi čia paminėti funkcijos apibrėžimo variantai vienaip ar kitaip pasirodo matematikos ir taikomosios matematikos srityse, bei skirtingų lygių matematikos mokymo institucijose.

Apibrėžiant funkciją iš objektų aibės $X$ į objektų aibę $Y$ kintamuoju vadinamas objektas, kuris laisvai pasirenkamas iš $X$ arba iš $Y$ . Sakoma, kad kintamojo reikšmės priklauso aibei $X$ arba aibei $Y$ , kurios vadinamos atitinkamo kintamojo reikšmių sritimis. Mus domina atvejis kai objektų aibės yra skaičių aibės. Gali būti, kad su bet kuria kintamojo x reikšme iš aibės $X$ yra susijusi (associated) apibrėžta (definite) kito kintamojo reikšmė y iš aibės $Y$ . Tuo atveju sakoma, kad y yra kintamojo x funkcija ir rašoma $y=f(x)$ . Šios kintamojo ir funkcijos sampratos paimtos iš R. Courant ir H. Robbins elementariosios matematikos vadovėlio [3; 274 pusl.], kuris buvo populiarus praėjusio amžiaus viduryje anglakalbėje literatūroje.

Panaši kintamojo ir funkcijos sampratos buvo naudojamos ir rusakalbėje literatūroje, pavyzdžiui, Fichtengolco tritomyje [7; 95 pusl.]. Tegul duoti du kintamieji x ir y su reikšmių sritimis $X$ ir $Y$ . Tarkime, kad kintamasis x gali įgyti bet kurią reikšmę srityje $X$ be jokių apribojimų. Tada kintamasis y vadinamas kintamojo x funkcija jo reikšmių srityje $X$ , jei pagal kurią nors taisyklę arba dėsnį kiekvienai x reikšmei iš $X$ priskiriama atitinkama y reikšmė (iš $Y$ ). Faktas, kad y yra x funkcija žymimas $y=f(x)$ , $y=\phi(x)$ , $y=F(x)$ ir t.t.

Toliau Fichtengolco vadovėlyje rašoma [7; 98 pusl.], kad paprasčiausias ir natūraliausias būdas nusakyti funkciją apibrėžiančią taisyklę analitiniu reiškiniu arba formule. Kiekvienas analitinis reiškinys turi savo natūralią apibrėžimo sritį; tai visų kintamojo x reikšmių aibė su kuriomis reiškinys turi prasmę. Tuo tarpu funkcijos apibrėžimo sritis gali skirtis nuo ją apibrėžiančio reiškinio natūraliosios apibrėžimo srities. Išeiti iš funkcijos apibrėžimo srities negalima, nors reiškinys gali turėti prasmę ir kitur.

Funkcijos sąvoka suteikia galimybę matematiškai tiksliai apibūdinti judėjimą. Matematinė funkcija yra sąryšis ar dėsningumas siejanti(s) kintamuosius dydžius. Tokia sąsaja nereiškia jokio priežastinio ryšio tarp kintamųjų.

Pagal R. Courant ir H. Robbins [3; 276 pusl.], matematikai ir fizikai sureikšmina skirtingus funkcijos sąvokos aspektus. Pirmieji paprastai akcentuoja atitiktį tarp kintamųjų. Šia prasme $f$ arba $f(\,\,)$ yra simbolis žymintis matematinę operaciją. Reikšmė $y=f(x)$ yra operacijos $f(\,\,)$ taikymo kintamajam x rezultatas. Tuo tarpu antruosius, fizikus, labiau domina pats dydis y negu matematinė operacija, kurios pagalba y apskaičiuojamas pagal x. Toks požiūris į funkciją dominuoja kai matematika taikoma fizikoje arba inžinerijoje. Tam, kad išvengti nesusipratimo dėl funkcijos traktavimo verta tiksliai nurodyti ar funkcija laikoma matematinė operacija $f$ kintamajam x priskirianti reikšmę $y=f(x)$ , ar funkcija yra pats kintamasis dydis y, kuris tarp kitko gali priklausyti visai nuo kito nepriklausomo kintamojo. Pavyzdžiui, skritulio plotas gali būti išreiškiamas funkcija $y=f(x)=\pi x^2$ , kai x yra skritulio spindulys, arba funkcija $y=g(z)=z^2/(4\pi)$ , kai z yra skritulio perimetras.

Šio amžiaus pradžios mokomoji matematinė literatūra gerokai pasikeitė. Pavyzdžiui, funkcijos apibrėžtis įgijo naujų atspalvių, atitinkančių Bourbaki funkcijos sampratą. Pagal E.D. Bloch [2; 131 pusl.], turint aibes $X$ ir $Y$ , funkcija $f$ iš $X$ į $Y$ , žymima $f\colon\,X\to Y$ , yra poaibis $F\subset X\times Y$ , jei kiekvienam $x\in X$ aibėje $F$ egzistuoja viena ir tik viena sutvarkyta pora $(x,y)$ . Šioje apibrėžtyje nėra paminėta funkcijos reikšmė $f(x)$ . Bet ji vienareikšmiškai apibrėžiama $f(x):=y$ naudojant antrąjį sutvarkytos poros $(x,y)$ elementą y.

Pastarajame universitetinės matematikos vadovėlyje rašoma [2; 133 pusl.], kad frazė ,,tegul $f(x)$ yra funkcija“ klaidinga. Jei funkcija yra $f\colon\,X\to Y$ , tai funkcijos vardas yra $f$ , o ne $f(x)$ . Simbolis $f(x)$ žymi funkcijos $f$ reikšmę atitinkančią argumentą x. Todėl $f(x)$ yra aibės $Y$ elementas, o ne funkcijos vardas. Tokia vienareikšmė pastaba reiškia funkcijos simbolių naudojimo praktikos kaitą. Apie kintamojo terminą taip pat pasisakoma vadovėlyje. Simbolis $f(x)$ klaidingai interpretuojamas kaip funkcijos vardas todėl, kad x yra ,,kintamasis“, o ne konkretus aibės $X$ elementas.

Panašios funkcijos sampratos laikomasi ir kai kurių šalių mokyklinės matematikos vadovėliuose, bei tarptautinio bakalaureato vadovėliuose.

Dalis mūsų šalies vadovėlių apibrėždami matematines sąvokas siekia apimti kuo daugiau apibrėžiamos sąvokos savybių. Funkcijos atveju tai iliustruoja sekanti vadovėlio ištrauka.

Pagal šią ištrauką, funkcija yra funkcinė priklausomybė, y (ygrekas), taisyklė, reiškinys, priklausomas kintamasis. Tokia sąvokos apibūdinimo įvairovė yra tipiška mūsų vadovėliuose, neva tokia apibrėžties forma padeda mokiniui geriau suprasti. Bet tokia apibrėžties forma netinkama kai sąvoka naudojama samprotavimui ir kitoms sudėtingesnėms funkcijos savybėms.

Iš dalies tokia apibūdinimų įvairovė yra perimta iš akademinės matematikos ir matematikos aukštosioms mokykloms. Funkcijos tapatinamas su taisykle $f$ ir su funkcijos reikšme $f(x)$ suprantamas minėtose bendruomenėse. Tai aiškinama teigiant, kad ,,[t]oks simbolio $f(x)$ dvilypumas nesudaro keblumų, nes jo prasmė paprastai būna aiški iš konteksto [9; 21 pusl.]. Tačiau matematikos naujokui tos prasmės kontekste nėra pažįstamos. Galima sutikti su minėtu Annos Sfard vaizdingu mokytojo apibūdinimu žongliruojančiu mokiniui nematomais daiktais-prasmėmis.

Kai kurie terminai funkcijos apibrėžtyje nėra paaiškinami. Mokiniui tenka tokių terminų prasmes perimti iš kitų kontekstų ir temų. Tokio termino pavyzdžiu yra ,,kintamasis“. Akademinėje matematikoje šis terminas nėra matematinis objektas, jis naudojamas kaip kalbos priemonė, reiškianti bet kurį kurios nors aibės elementą. Mūsų mokyklinėje matematikoje kintamasis naudojamas ir temose susijusiose su programavimu, ir temose susijusiose su statistika.

Kintamasis statistikoje apibūdinamas taip [4; 17 pusl.]. Statistinio tyrimo objektų grupę, kartu ir imties elementus vienija tiriamasis požymis. Matuodami šį požymį, gauname tam tikra dydį, kuris kinta kartu su imties nariais. Šis dydis vadinamas statistiniu kintamuoju arba tiesiog kintamuoju. Amžius, lytis, namų ūkio pajamos ir išlaidos, galvos apimtis, transporto priemonės tipas yra kintamųjų pavyzdžiai.

Kintamasis programavime suprantamas dar kitaip. Duomenys, kurių reikšmės gali keistis atliekant programą, vadinami kintamais duomenimis, arba tiesiog kintamaisiais. Kintamasis – programos objektas, nusakomas vardu ir reikšme, kuri gali būti naudojama ir keičiama. Kintamojo x reikšmę keičiančios komandos pavyzdys: $x = x + 2$ . Palygink šį užrašą su lygties samprata.

Kintamojo prasmė daugumoje mūsų vadovėlių yra miglota ir priklauso nuo konteksto. Todėl kelia sunkumų mokiniams. Mokytojai turėtų į tai atsižvelgti. Funkcijos sąvokos daugiaprasmiškumas persikelia išvestinės funkcijos sąvokai.

Šioje ištraukoje rašoma apie ,,išvestinę funkciją $y=f'(x)$ ir apie ,,reiškinio $f(x)$ išvestinę“, tapatinamą su reiškiniu $f'(x)$ . Turintiems matematinę patirtį, funkcijos ir reiškinio nagrinėjimas pakaitomis ar jų tapatinimas, reikia manyti problemų nesukelia. Nors dėl skirtingo apibrėžimo srities traktavimo toks tapatinimas yra klaidingas. Be to, naujokui toks tapatinimas gali trukdyti funkcijos sąvokos kaip matematinio objekto formavimuisi.

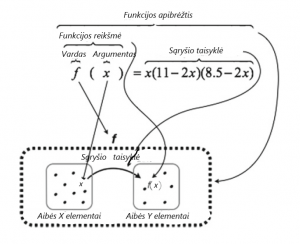
Šios vadovėlių ištraukos leidžia spėti, kad jų autorių nuomone visas simbolis $f(x)$ yra funkcijos vardas. Toks požiūris paplitęs tarp matematikos mokytojų ir kitose šalyse [8]. Tuo tarpu matematiškai korektišką funkcijos simbolio sampratą vaizduoja sekanti schema.

Funkcijos simbolis pagal [8]

Du funkcijos sąvokos supratimo aspektai

Toliau aptarsime funkcijos supratimo pedagoginį aspektą. Pirmą kartą mokiniui susidūrus su funkcijos Dirichlet-Bourbaki apibrėžtimi, ji nėra suvokiama kaip matematinis objektas, t.y. suvokiama kaip daiktas su kuriuo galima atlikti matematinius veiksmus. Matematiko mokymo tyrėjai sutaria, kad matematinių objektų supratimas vystosi etapais. Procesas ir objektas yra du pagrindiniai tokio supratimo vystymosi etapai ([1], [10]).

E. Dubinsky ir jo kolegos išplėtojo matematinio supratimo prigimties ir jo vystymo teoriją. Šios teorijos požiūriu supratimas vystosi nuosekliai pereidamas keturis etapus: veiksmas, procesas, objektas ir schema. Šių etapų pavadinimų pirmosios raidės naudojamos teorijos pavadinimui VPOS (angl. APOS). Paaiškinsime VPOS teoriją funkcijos supratimo atvejui pagal [6]. Veiksmas yra pirmasis supratimo etapas, reiškiantis gebėjimą įstatyti skaičių į reiškinį ir apskaičiuoti rezultatą. Kartojant ir apmąstant skaičiavimo veiksmą, jis gali tapti vidiniu psichiniu procesu. Procesas atlieka tą pačią operaciją kaip ir veiksmas tik vyksta mąstant ir įsivaizduojant kiekvieną skaičiavimo etapą. Kai individas pilnai įsisąmonina visą procesą, geba atlikti aritmetinius veiksmus su funkcijomis ir tuo būdu gauna naują funkciją, procesas yra supresuojamas (encapsulated) į objektą. Vystantis kurios nors temos apie funkcijas supratimui, kai individas konstruoja veiklas, procesus ir objektus susijusioms sąvokoms ir apjungia visą tai į struktūrą, pasiekiamas ketvirtasis etapas vadinamas funkcijos temos schema. Suderinta funkcijos schema gali būti Dirichlet-Bourbaki funkcijos apibrėžtis, apimanti apibrėžimo sritį, reikšmių sritį ir elementų priskyrimo taisyklę. Toks funkcijos supratimo lygis įgalintų individą suvokti funkciją užduotyse, kuriose ji nėra tiesiogiai minima.

Perėjimas nuo funkcijos kaip proceso prie funkcijos kaip objekto nėra paprastas ir trumpas. Toks perėjimas gali niekada neįvykti. Funkcijos kaip objekto supratimas yra labai svarbus ne tik pačioje matematikoje, bet ir taikomojoje matematikoje. Pavyzdžiui, epidemijos sklidimo eksponentiniu greičiu supratimas remiasi laipsninių funkcijų ir eksponentinių funkcijų globalių savybių skirtumų supratimu.

E. Dubinsky ir G. Harel rinkinyje [5] apžvelgti darbai atlikti funkcijos sąvokos tyrimų srityje iki 1992 metų. Viename iš šio rinkinio straipsnių [11] A. Sfard plėtoja savąją trijų etapų matematinio objekto supratimo teoriją funkcijos atveju. Jos aprašytos apklausos pirmąjį klausimą uždaviau mūsų mokytojams.

Apklausa ir jos rezultatai

Apklausa atlikta siekiant išsiaiškinti keletą dalykų. Pirma, kokiai mokytojų daliai funkcija greičiau yra skaičiavimo procesas, o kokiai mokytojų daliai funkcija greičiau yra objektas (lentelė)? Antra, kurią iš trijų funkcijų sumos diferencijavimo formulių mokytojai laiko geriau atitinkančia išvestinės sąvoką? Remiantis apklausos rezultatais atliksime statistinį tyrimą siekdami išsiaiškinti: Ar atsakymas į antrąjį klausimą priklauso nuo atsakymo į pirmąjį klausimą?

Mokytojams pasiūlyta atsakyti į sekančius du klausimus pasirenkant nurodytus atsakymo variantus.

Kuris iš dviejų sekančių sakinių, jūsų nuomone, geriau apibūdina funkcijos sąvoką?
1. Funkcija yra skaičiavimo procesas, kuriuo kiekvienam skaičių aibės elementui, pagal žinomą taisyklę, apskaičiuojama reikšmė.
2. Funkcija yra tam tikros rūšies (galimai begalinė) lentelė, kurioje vienos skaičių aibės elementą atitinka kitos skaičių aibės elementas.
Kuri iš trijų sekančių formulių, jūsų nuomone, geriau atitinka išvestinės sąvoką?
1. $(f(x)+g(x))'=f'(x)+g'(x).$
2. $(f+g)'(x)=f'(x)+g'(x).$
3. $(f+g)'=f'+g'.$

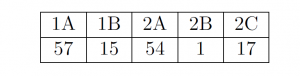
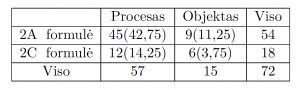
Iš 73 užsiregistravusių seminare mokytojų, apklausoje dalyvavo visi. Kiekvieno atsakymo rezultatu yra sutvarkyta pora, kurios pirmasis narys yra pasirinkimas pagal pirmąjį klausimą, o antrasis narys yra pasirinkimas pagal antrąjį klausimą. Viso galimų skirtingų atsakymų yra šešios poros ir jų pasirinkimų rezultatai pavaizduoti pirmoje lentelėje. Vieno respondento atsakymas neatitiko pasiūlytos formos, todėl jo rezultatas neatsispindi lentelėje.

Kitoje lentelėje pavaizduoti kiekiai mokytojų balsavusių už kiekvieną iš penkių pasirinkimų.

A dalies pirmajame klausime pasirinkimų gausa rodo, kad $79\%$ mokytojų funkciją traktuoja kaip skaičiavimo procesą, o ne kaip objektą su kuriuo galima elgtis kaip, pavyzdžiui, su skaičiais. A dalies antrajame klausime pasirinkimų gausa rodo, kad $75\%$ mano, kad funkcijos sumos išvestinės sąvoką geriau atitinka pirmoji formulė. Ši formulė yra prieštaringa, galimai keliomis prasmėmis. Pavyzdžiui, kairią formulės pusę galima suprasti kaip ,,kintamojo x reiškinio“ išvestinę, o dešinę formulės pusę galima suprasti kaip išvestinių funkcijų $f'$ ir $g'$ reikšmių taške x sumą.

Šie apklausos rezultatai yra labai svarbūs siekiant įvertinti mokytojų supratimą apie funkciją kaip mokyklinės matematikos sąvoką. Remiantis anksčiau minėtomis matematikos mokymo tyrimų teorijomis, galima daryti išvadą, kad dauguma mokytojų neturi galutinai susiformavusios sampratos apie funkcijas, kaip matematinius objektus.

Statistinis tyrimas

Tyrimu bandome išsiaiškinti, ar atsakymas į antrąjį klausimą priklauso nuo atsakymo į pirmąjį klausimą? Kitaip tariant, ar funkcijų sumos diferencijavimo simbolinės formos pasirinkimas priklauso nuo funkcijos traktavimo procesu vs objektu.

Statistiniam tyrimui naudojame chi-kvadrato statistiką, kurios pagalba vertinsime dviejų kategorinių kintamųjų asociaciją toje pačioje imtyje. Tyrimo nulinė hipotezė – du kategoriniai kintamieji, matematinio objekto statusas ir matematinė simbolika, yra nepriklausomi. Alternatyvi hipotezė – atsakymas į antrąjį klausimą priklauso nuo atsakymo į pirmąjį klausimą.

$\chi^2(1,n=72)=2,273<2,7$ , p-reikšmė $>0,1.$ Esant reikšmingumo lygmeniui $\alpha = 0,05$ , imties duomenys neprieštarauja nulinei hipotezei, t.y. apklausos rezultatai rodo, kad matematinės simbolika sumos diferencijavimo formulėse nepriklauso nuo požiūrio į funkciją.

Statistinio tyrimo rezultatas rodo, kad atsakymas į antrąjį klausimą nėra reikšmingiau susijęs su atsakymu į pirmą klausimą. Kaip tai paaiškinti?

Jei tikėtis nuoseklumo matematinėje simbolikoje, tai 2A formulė gali pasirodyti tada, kai funkcija laikoma reiškiniu, sietinu su skaičiavimo procesu, o simbolis $f(x)$ traktuojamas kaip funkcijos vardas. Funkcijų suma šiuo atveju taip pat yra reiškinys žymimas simboliu $f(x)+g(x)$ , o išvestinė žymima $(f(x)+g(x))'$ . Tuo tarpu 2B ir 2C formulės turėtų pasirodyti tada, kai funkcija laikoma objektu ir funkcijų suma apibrėžiama kaip funkcija $f+g$ su reikšmėmis $(f+g)(x):=f(x) + g(x)$ visiems argumentams x iš bendros $f$ ir $g$ apibrėžimo srities. Funkcijos sumos išvestinė šiuo atveju yra funkcija $(f+g)'$ su reikšmėmis $(f+g)'(x)$ visiems x kaip ir anksčiau. Statistinio tyrimo rezultatu galima laikyti nenuoseklumo matematinėje simbolikoje egzistavimo patvirtinimą.

Nenuoseklumas matematinėje simbolikoje aptinkamas ir vadovėliuose.

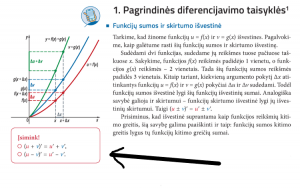
Šioje ištraukoje yra keletas svarbių momentų. Pirma, funkcijos $u=f(x)$ ir $v=g(x)$ turi po du skirtingus vardus $(u,f)$ ir $(v,g)$ , atitinkamai, nepaaiškinant to prasmės. Antra, abiejų funkcijų grafikai brėžiami koordinačių sistemoje $yOx$ . Trečia, abiejų funkcijų sumos išvestinės žymimos $(u+v)'$ ir $(f(x)+g(x))'$ . Abi formulės yra to paties vadovėlio gretimuose puslapiuose.

Atnaujinamos matematikos programos peržiūros seminare vykusiame 2022 metų gegužės 26 dieną buvo pasiūlyta programoje esančią formulę 2A keisti į 2B arba 2C. Šis siūlymas nebuvo priimtas. Atlikta vadovėlių apžvalga ir mokytojų apklausa rodo, kad siūlymas buvo ankstyvas, daugumos mokytojų požiūris į funkciją yra pradinėje formavimosi stadijoje.

Šio teksto samprotavimų išvada: mokytojai turėtų būti supažindinami su matematinių objektų supratimo sudėtingumu, reikalaujančiu iš besimokančiojo nuosekliai pereiti kelias supratimo stadijas, nuo proceso prie objekto. Nuoseklus mokymosi kelias turėtų būti numatytas matematikos programoje visoms sąvokoms, ne tik funkcijos. Detaliai apie matematinių objektų supratimo problemas rašoma tam skirtoje knygoje [1] ir daugelyje kitų darbų.

Patarimai mokytojams

Kiti patarimai mokytojams apibendrinant tekstą.

Mažinti kiekį tokių užduočių, kurios klausia tik atsakymo ir didinti kiekį užduočių, kurios reikalautų paaiškinti pagrindžiant ar įrodant.

Siekti formuluoti ir naudoti matematines apibrėžtis su joms būdingomis savybėmis.

Matematinės sąvokos supratimas besimokančiajam turi kelias supratimo stadijas: procesas, kompaktiškas procesas, daiktas-objektas. Atsižvelgiant į tai galima būtų bandyti įvertinti mokinių individualius sąvokų įvaizdžio ir sąvokų supratimo skirtumus.

Atkreipti mokinių dėmesį į funkcijos pavyzdžius skirtingose temose: figūrų transformacijos geometrijoje, aritmetiniai veiksmai aritmetikoje, lygties sprendimas, grafikai, lentelės atspindinčios dydžių priklausomybę, funkcinių ryšių pavyzdžius realaus pasaulio patirtyse (nuvažiuotas kelias, įpiltas benzinas ir t.t.). Iš turimų funkcijų formuoti naujas funkcijas, pvz. funkcijų suma.

Galiausiai patarimas matematikos vadovėlių autoriams. Svarbiu vadovėlio privalumu turėtų būti logikai skirto skyrelio gale suformuluotų penkių mokyklinės matematikos principų laikymasis.

Literatūra

I. Arnon, J. Cottrill, E. Dubinsky, A. Oktac, S. Roa Fuentes, M. Trigueros, K. Weller. APOS theory: a framework for research and curriculum development in mathematics education. Springer,
E.D. Bloch. Proofs and Fundamentals. A First Course in Abstract Mathematics. Second Edition. Springer, 2011.
R. Courant, H. Robbins, I. Stewart. What is Mathematics? An Elementary Approach to Ideas and Methods. Second Edition. Oxford University Press, 1996.
V. Čekanavičius ir G. Murauskas. Statistika ir jos taikymai. I. TEV, 2001.
E. Dubinsky and G. Harel (Eds.). The Concept of Function. Aspects of Epistemology and Pedagogy. Mathematical Association of America, 1992.
E. Dubinsky. Actions, Processes, Objects, Schemas (APOS) in Mathematics Education. In: S. Lerman (Ed.). Encyclopedia of Mathematics Education. Second Edition. Springer, 2020, pp. 16-19.
G. Fichtengolcas. Matematinės analizės pagrindai. I. ,,Mintis“, 1965. (Cituojama pagal originalą rusų kalba).
S. Musgrave and P.W. Thompson. Function notation as idiom. In: P. Liljedahl and C. C. Nicol (Eds.), Proceedings of the 38th Meeting of the International Group for the Psychology of Mathematics Education. (Vol. 4, pp. 281–288). Vancouver, BC: PME.
V. Pekarskas. Diferencialinis ir integralinis skaičiavimas. I dalis. Technologija, 2008. A. Sfard. On the dual nature of mathematical conceptions: reflections on processes and objects as different sides of the same coin. Educational Studies of Mathematics. 1991, vol. 22, 1–36.
A. Sfard. On the dual nature of mathematical conceptions: reflections on processes and objects as different sides of the same coin. Educational Studies of Mathematics. 1991, vol. 22, 1–36.
A. Sfard. Operational origins of mathematical objects and the quandary of reification – the case of function. In: E. Dubinsky, G. Harel (Eds.). The Concept Of Function. Aspects of Epistemology and Pedagogy. Mathematical Association of America, 1992.
A. Sfard. The long way from mathematics to mathematics education. How educational endeavor may change one’s vision of mathematics \& of its development. Presentation in International Congress of Mathematicians, 11 Jun 2022. \url{https://www.youtube.com/watch?v=GNujXdZ3y6g}
B. Sriraman and K. Umland. Argumentation in Mathematics Education. In: S. Lerman (Ed.). Encyclopedia of Mathematics Education. Second Edition. Springer, 2020, pp. 63-66.
V. Stakėnas. Matematikos istorijos skiautiniai. Tikros istorijos apie matematikus ir jų mokslą. Žara, 2017.
Hung-Hsi Wu. Teaching School Mathematics: Algebra. American Mathematical Society, 2016.

Matematika kaip kultūros reiškinys