Aptarsime tris priežastis dėl kurių matematinis įrodymas yra svarbus jau pradinukams ir paaiškinsime vieną stereotipą apie matematinį įrodymą.
Pirmoji priežastis – atpažinti mąstymo klaidas.
Antroji priežastis – iš ugdymo filosofijos srities.
Trečioji priežastis – EBPO švietimo politika.
Stereotipas – matematinis įrodymas yra tik teiginio teisingumo pagrindimas, turintis griežtą loginę struktūrą.
Pirmoji priežastis – atpažinti mąstymo klaidas
Matematikoje įprasta susidurti su dėsningumais, kurie galimai galioja be galo dideliam objektų kiekiui. Kaip įsitikinti, kad dėsningumas kartojasi be galo daug kartų? Mokykloje labai dažnai dėsningumas patikrinimas keliems pavyzdžiams ir paliekama manyti, kad jis teisingas visiems kurios nors begalinės klasės elementams. Deja, tokiu būdu pratiname prie mąstymo klaidų, kurios ateityje tampa įpročiu.
Davis (1981) pavyzdys rodo kokių keistų gali būti situacijų. Atrodytų paprastas reiškinys
čia
yra natūralusis skaičius.
Klausimas: Ar šis reiškinys yra kokio nors natūraliojo skaičiaus kvadratu? Kitaip tariant: Ar su kiekvienu galima rasti tokį natūralųjį skaičių
kad
?
Su kompiuterio pagalba buvo įsitikinta, kad atsakymas į klausimą yra neigiamas visiems nuo 1 iki 30 693 385 322 765 657 197 397 207. Bet, sekanti natūraliojo skaičiaus
reikšmė atsakymą paneigia;
yra lygus natūraliojo skaičiaus kvadratui kai
reikšmė tampa vienetu didesnė už paskutinę.
Šis pavyzdys rodo, kad, esant be galo dideliam objektų kiekiui, nuoseklus dėsningumo tikrinimas gali niekada nesibaigti. Matematikos šiuolaikine prasme atsiradimas siejamas su tokiu samprotavimo būdo radimu, kuris leidžia įsitikinti dėsningumo galiojimu be galo dideliam objektų skaičius. Turime galvoje nebendramačių dydžių egzistavimo problemos sprendimą Senovės Graikijoje. Įrodymu vadinamas samprotavimo būdas sukūrė tai, ką dabar vadiname matematika.
Kaip toks samprotavimas veikia paaiškinsime nagrinėdami natūraliojo skaičiaus savybę – jo (ne)dalumą iš dviejų.
Pirmas klausimas: Kaip apibrėžiama (ne)dalumo iš dviejų savybė? Tarkime, kad pradinukas supranta skaičių, kaip nuoseklaus skaičiavimo pabaigą ir tuo pačiu būdu skaičius sudeda. Būtent, pradinukams skaičius yra tai, kas gaunama nuoseklaus skaičiavimo gale.Pavyzdžiui, ,,Skaičiuoti devynis žingsnius pradedant 0“ reiškia ėjimą nuo 0 prie 1, taip toliau, nuo 8 prie 9:
0 → 1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9
Pradinukams skaičių suma yra nuoseklaus skaičiavimo pratęsimas. Pavyzdžiui, 4 plius 5 reiškia tokį skaičių, kuris gaunamas ,,skaičiuojant 5 žingsnius pradedant 4“ :
4 → 5 → 6 → 7 → 8 → 9
Paskutinis gaunamas skaičius, šiuo atveju 9, yra suma 4 + 5.
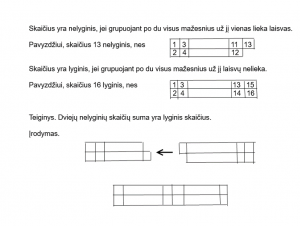
Apibrėžimas. Skaičius yra nelyginis, jei, nuosekliai skaičiuojant ir grupuojant po du visus ne didesnius už jį, vienas lieka laisvas. Skaičius yra lyginis, jei, nuosekliai skaičiuojant ir grupuojant po du visus ne didesnius už jį, laisvų nelieka.
Antras klausimas: Kokie dėsningumai būdingi lyginiams ir nelyginiams skaičiams? Pavyzdžiui, kas atsitinka sudedant du nelyginius skaičius?
Žvilgterėkime į paprasčiausius pavyzdžius: 1+3=4, 5+9=14,…… Galima pastebėti ir spėti esant teisingam tokį dėsningumą.
Teiginys. (Bet kurių) dviejų nelyginių skaičių suma yra lyginis skaičius.
Ar pavyzdžiai įrodo šį teiginį?
- Kas jei imsime didelių skaičių porą: 3579+1641=5220,….
- Dviejų lygių skaičių porą: 31+31=62,……
- Du pirminius nelyginius: 7+11=18,…. .
Problema – yra be galo daug pavyzdžių. Visų jų patikrinti neįmanoma.
Teiginio įrodymas.Jei sudėsime du nelyginius skaičius, tai nuosekliai skaičiuodami ir poruodami gausime du laisvus (be poros) skaičius. Bet likę du laisvi skaičiai sudarys naują porą ir laisvų neliks. Taigi, sudėjus du nelyginius gavome skaičių, kuris būdamas nuoseklaus skaičiavimo rezultatu visus iki jo pavyksta sugrupuoti po du.Todėl nelyginių skaičių suma yra lyginis skaičius.
Jei lyginio ir nelyginio skaičiaus apibrėžimus iliustruosime piešiniais, tai tą patį galima padaryti ir su jo įrodymu.
Mokiniui įsisavinant vis abstraktesnes sąvokas tos pačios savybės apibrėžiamos skirtingais būdais. Todėl atitinkamų dėsningumų įrodymai tampa abstraktesni ir logiškai sudėtingesni.
Apibrėžtis. Natūralusis skaičius yra nelyginis, jei
su kuriuo nors natūraliuoju skaičiumi
. Natūralusis skaičius
yra lyginis, jei
su kuriuo nors natūraliuoju skaičiumi
.
Sudėdami du nelyginius skaičius ir
gauname
Gauta sumos išraiška rodo ją esant lyginiu natūraliuoju skaičiumi.
Apibendrinsime tai kas iki šios vietos sakyta. Dėsningumo įrodymas priklauso nuo klasės bendruomenės turimo žinių lygio.
Apibrėžtis. Įrodymu vadinamas matematinis argumentas, kurį sudaro matematinį teiginį patvirtinančių arba paneigiančių susijusių teiginių seka, turinti šias tris savybes:
- Naudoja teiginius, kurie klasės bendruomenei žinomi kaip teisingi ir nereikalauja papildomo pagrindimo;
- Taiko tokias samprotavimo formas, kurios galioja ir klasės bendruomenei yra žinomos arba nesunkiai išvedamos;
- Formuluojama tomis reiškimo formomis, kurios yra tinkamos ir klasės bendruomenei yra žinomos arba nesunkiai gaunamos.
Antroji priežastis – iš ugdymo filosofijos srities
Filosofinis argumentas:
- Pirma, norime supažindinti su matematika.
- Antra, jei norime supažindinti su dalyku, tai, nuo pat mokymo pradžios, turėtume mokyti to dalyko esmines savybes (struktūrą ir logiką).
- Trečia, įrodymas yra matematikos esminė savybė (siela).
- Išvada: su įrodymu turėtume pradėti supažindinti jau pradinukus.
Tai yra pagrįstas argumentas. Tai reiškia, kad išvada teisinga, kai teisingos visos trys prielaidos.
Pirmosios prielaidos teisingumas priklauso nuo švietimo politikos. Mūsų švietimo politikos epizodai neigiantys pirmosios prielaidos teisingumą (citata iš 2009 straipsnio):
„Atsisakyti dalykais ir mokslo logika išdėstyto ugdymo turinio yra nelengva, tačiau neišvengiama, jeigu siekiame, kad vaikas iš tikrųjų būtų „centre“, kad atsižvelgtume į jo mokymosi logiką, poreikius ir galias.“
Kita ištrauka iš ministro įsakymo (2007):
9. Pagrindinės ugdymo turinio silpnybės.
9.1. Visais švietimo lygmenimis formuojamas ir įgyvendinamas ugdymo turinys išlieka pernelyg orientuotas į žinias ir mokinių akademinių gebėjimų ugdymą ….
Švietimo politikos prošvaistes rodo ši ištrauka iš ministro įsakymo dėl ugdymo turinio atnaujinimo Gairių (2019):
40. Dalyko turinys sudaro sąlygas ugdytis kompetencijas, bendrojoje programoje jis pateikiamas nuosekliai, atsižvelgiant į atitinkamo mokslo akademinę logiką, metodologiją ir paisant mokinių amžiaus tarpsnio ypatumų.
Pedagoginis argumentas:
Pirma, matematinis įrodinėjimas yra būtinas giliam matematikos mokymui.
Antra, jei norime, kad mokiniai suprastų matematiką, tai jos mokymas turi būti gilus.
Trečia, norime, kad mokiniai suprastų matematiką.
Išvada: matematikos pamokoje turime įrodinėti.
Pirma prielaida gali būti kvestionuojama. (Tik) matematikos taikymas realiam pasauliui yra būtinas giliam matematikos mokymui.
Įrodymas yra įmanomas kai žinios turi griežtą hierarchinę struktūrą. Ją palaiko matematinis samprotavimas mokykloje:
- kiekviena sąvoka yra apibrėžiama;
- kiekvienas teiginys yra nedviprasmiškas ir formuluojamas taip, kad būtų aišku, kas yra žinoma ir kas nėra žinoma;
- kiekvienas teiginys yra pagrindžiamas logiškai taisyklingu samprotavimu (įrodymu);
- kiekviena nauja sąvoka formuojama turimų žinių pagrindu ir yra naujų žinių struktūros dalimi;
- matematikos žinios yra orientuotos į tikslą ir sprendžia kurią nors problemą.
Matematinio samprotavimo pavyzdys.
Apibrėžtis. Skaičius yra taškas (skaičių) tiesėje.
Apibrėžtis. Teigiamų skaičių a ir b suma a+b yra dešinysis galas intervalo, gaunamo apjungus vieną greta kito padėtus intervalus [0,a] ir [0,b]:
|———–|————–|————->
0 a a+b
Teorema. Trupmenų ir
suma yra trupmena
.
Įrodymas. Intervalus ir
nuosekliai padaliname
ilgio intervalais ir suskaičiuojame kiek jų telpa.
Trečioji priežastis – EBPO švietimo politika
Mūsų švietimo politika tapo priklausoma nuo EBPO švietimo politikos dar gerokai iki Lietuvai tapus pilnateise jos nare 2018 metais. Todėl EBPO švietimo standartai mums turi didelę įtaką. Trumpai apie šiuos standartus mokyklinės matematikos srityje.
Mokyklinės matematikos turinio centre yra
matematinis samprotavimas ir problemų sprendimas (!).
Kaip EBPO supranta problemų sprendimą?
Tai sprendimų paieška nepažįstamose situacijose.
Tai gebėjimas užsiimti pažintine paieška siekiant suprasti ir išspręsti tokias situacijas, kurios metodų ir sprendimų atžvilgiu nėra akivaizdžios.
Jis yra daugiaplanis ir daugiamatis, apima tarpasmeninių, vidinių asmeninių ir socialinių santykių sritis.
Mūsų programoje problemų sprendimas – žinomų metodų taikymas žinomose situacijose.
Visas matematikos turinys turėtų išreikšti 6-ias pagrindines idėjas (ne sritis!):
- Skaičių sistema ir jų algebrinės savybės;
- Matematika kaip abstrakčių sąvokų ir simbolinių išraiškų sistema;
- Matematika kaip hierarchinė struktūra;
- Funkciniais sąryšiais tarp dydžių;
- Matematinis modeliavimas kaip akiniai į realųjį pasaulį;
- Dispersija kaip statistikos esmė.
Matematinis samprotavimas tapo matematinio raštingumo pagrindine dalimi.2021 metų PISA tyrime 25% užduočių priklausys nuo grynosios matematikos žinių gilumo.Susikaupė pakankamai svarus pagrindimas to, kad grynoji matematika, net mokyklos lygmenyje, lemia pasiekimus sprendžiant užduotis realaus pasaulio kontekste.
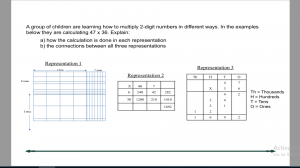
PISA 2021 užduoties pavyzdys. Daugyba 47×36 atliekama trimis skirtingais metodais. Paaiškinti:
- (a) kaip dauginama kiekvienu iš metodų;
- (b) ryšius tarp visų trijų metodų.
Įrodinėjimas yra prasmės kūrimo būdas matematikoje
Daugelis žmonių apie įrodymą turi vienareikšmę nuomonę – tai būdas įsitikinti, kad matematinis teiginys yra teisingas. Bet tai yra tik dalis tiesos. Ne mažiau svarbi yra kita įrodymo paskirtis – paaiškinti, kodėl teiginys teisingas. Ne visi įrodymai vienodai gerai atlieka pastarąją paskirtį. Todėl labai dažnai akademinėje matematikoje vienu to paties fakto įrodymu neapsiribojama. Ypač kai pirmasis įrodymas yra ilgas ir sudėtingas, nepaaiškinantis kodėl teiginys teisingas.
Kita stereotipo apie matematinį įrodymą dalis yra jo forma. Manoma, kad įrodymas turi atitikti tam tikrus formalius loginio taisyklingumo reikalavimus. Tačiau taip įrodymas suprantamas tada, kai jis pats yra matematinio tyrimo objektu. Praktiškai įrodyme visada būna tiesiogiai neįvardijamų samprotavimo dalių. Tokių dalių, kurias tos srities specialistas reikalui esant galėtų užpildyti. Įrodymo pilnumas priklauso nuo to, kam jis skirtas. Anksčiau apibūdintas mokyklinis įrodymas turi tą pačią savybę.
Deja, mokyklinėje matematikoje įrodymas dažnai vertinamas tik stereotipine prasme. Atiduodant duoklę vis dar pripažįstamai įrodymo svarbai, jis paprasčiausiai tampa ritualu, jo mokomasi mintinai. Ir šia prasme įrodymo reikalingumas kvestionuojamas, nes mokyklinės tiesos laikomos ir taip neabejotinai teisingomis.
Tačiau aiškinamoji įrodymo funkcija mokykloje yra ypatingai svarbi. Todėl mokykloje svarbu ieškoti tokių faktų ir jų įrodymo būdų, kurie paaiškintų to fakto teisingumą. Bandant įrodymus nukelti į paskutines klases ir nesirūpinti jų aiškinamąja funkcija reiškia atsisakymą tokiu būdu ieškoti prasmės matematikoje.
Pabaigai kelios pastabos. Dabartinė matematikos programa yra atskirų tarpusavyje mažai susijusių temų rinkinys. Matematikos mokymas orientuotas į mokinio parengimą atlikti nedidelį kiekį užduočių, parodančių gebėjimą atlikti standartines procedūras. Tai vadinama ,,akademinėmis žiniomis” ir teisingai vertinama kaip šių laikų poreikių neatitinkantis dalyko mokymas. Konstatavus šį faktą mūsų švietimo sistemoje bandoma mažinti matematikos dalyko dalį bendrajame lavinime.
Atsižvelgiant į tai kas sakyta aukščiau, būtų išmintinga keisti matematikos mokymą jį gilinant, o ne integruojant su kitais dalykais. Mokyklinis matematikos kursas turėtų apimti nedidelį kiekį fundamentalių matematikos idėjų. Pavyzdžiui, EBPO siūlo šešias tokias idėjas. Tuo tarpu skirtingos temos turėtų būti susijusios ta prasme, kad kiekviena iš jų atskleistų pagrindinių idėjų skirtingus aspektus. Bet reikia pripažinti, kad prieš tai turėtume pakeisti matematikos mokytojų rengimą.
Pagrindinės mokyklinės matematikos idėjos – kaip žmogaus griaučiai. Kaip raumenys ir kraujotaka veikia griaučius, taip uždaviniai suteikia gyvybę matematikai. Įrodymas matematikai yra tai, kas siela yra žmogui. Įrodymas įprasmina visas matematikos dalis. Manau, kad idėjos ir dėsningumo pasirinkimą nagrinėti klasėje turėtų lemti jos įrodymo paprastumas, efektyvumas ir grožis. Tokias savybes, pavyzdžiui, turi faktas, kad yra iracionalusis skaičius.
Teiginys. Jei (natūraliojo) skaičiaus kvadratas lyginis, tai pats skaičius taip pat lyginis.
- Implikacija – sudėtinis teiginys, kurio loginė forma ,,jei A, tai B“.
- Kada toks teiginys teisingas ar klaidingas?
- Įrodymas prieštaros būdu.
Literatūra
A.J. Stylianides. Proving in the elementary mathematics classroom. Oxford University Press, 2016.
D.A. Stylianou, M.L. Blanton, E.J. Knuth (eds). Teaching and Learning Proof Across the Grades. A K-16 Perspective. Routledge, 2009.
P.J. Davis. (1981) Are there coincidences in mathematics? American Mathematical Monthly, 88, 311-320.