Vakar įvyko Ukmergės matematikos mokytojų seminaras, kuriame tęsiau savo pokalbį su mokytojais apie racionaliuosius skaičius. Kaip ir ankstesniuose tokiuose seminaruose norėjau paaiškinti, kaip galima logiškai nepriekaištingai apibrėžti trupmenas ir pagrįsti aritmetinius veiksmus su racionaliaisiais skaičiais. Mano tikslas – suteikti gilesnes elementariosios matematikos žinias mokytojams. Taip darau todėl, kad tikiu, jog įgimtas vaikų smalsumas ir noras mokytis matematikos gali būti išsaugoti mokykloje jei jie supras tai, kas jiems sakoma.
Šie seminarai padeda man geriau suprasti mūsų matematikos mokymo problemas. Čia paminėsiu vieną problemą, kuri man atrodo svarbiausia. Mūsų matematikos mokytojai neturi gilių elementariosios matematikos žinių. Kitaip tariant, ruošdami matematikos mokytojus ir vėliau keldami jų kvalifikaciją, mes neskiriame pakankamo dėmesio matematikos turinio įsisavinimui. Mes suteikiame būsimiems mokytojams universitetinės matematikos turinio žinias ir matematikos didaktikos žinias, tikėdamiesi, kad jų pakaks mokyklinės matematikos turiniui suprasti. Tai ne mūsų vienų problema ir jau senai įtikinamai parodyta, kad nėra ko tikėtis sėkmės be specialių mokyklinės matematikos turinio studijų.
Man galima prieštarauti sakant, kad gal būt tai ir yra problema, bet vargu ar ji svarbiausia. Galima sakyti, kad be tinkamo visuomenės požiūrio į matematinį švietimą mes vargiai pasistumėsime net ir tuo atveju, kai mokytojai gerai paruošti. Šia prasme galima būtų sakyti, kad visuomenės požiūris į švietimą yra dar svarbesnis. Šiuo metu man atrodo, kad vienintelis realus kelias keisti visuomenės požiūrį yra matematikos mokytojo kvalifikacijos kėlimas. Todėl mokyklinės matematikos turinio problematiką laikau svarbiausia.
Mano nuomone, absoliuti dauguma mokinių pirmoje klasėje turi norą mokytis matematikos. Motyvacija mokytis matematikos prarandama mokykloje palaipsniui. Motyvacijos praradimas turėtų būti juntamas tarp 6-7 klasės mokinių ir vėlesnėse klasėse tokių mokinių turėtų tik daugėti. Baigiamosiose klasėse dauguma mokinių jau yra praradę viltį suprasti matematiką, o dažnas jos nekenčia ar bijo. Nereikia specialių tyrimų norint įsitikinti, kad tokių mokinių tikrai turime ir nemažai. Norėdami spręsti šią problemą rūpinamės, kaip suprantamiau paaiškinti analizės pagrindų ir algebros sąvokas. Tačiau taip elgtis, reiškia kovoti su pasekmėmis. Tam, kad sumažinti ar net išvengti tokių reiškinių vyresnėse klasėse, reikia rūpintis pradinių klasių matematikos mokymo turiniu.
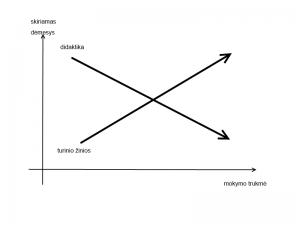
Kaip minėjau, pastarasis teiginys apie matematikos turinio svarbą nėra akivaizdus ir dažnai ginčijamas didaktikos naudai. Sprendžiat pagal mokytojų ruošimo tradicijas, manoma, kad pradinių klasių mokytojams nėra būtinos gilios matematikos žinios. Pradinių klasių mokytojų ruošime dominuoja didaktikos žinių suteikimas. Toks pat santykis tarp dėmesio didaktikai versus turiniui pasireiškia ir ruošiantis pamokoms. Matematikos mokytojas Benas Orlinas šią situaciją pavaizdavo taip:
Tačiau, jau pradinėse klasėse vaikas susipažįsta su svarbiausia matematikos sąvoka – skaičiumi. Kažką ne banalaus apie skaičių galima pasakyti žinant daug kartų daugiau negu rašoma vadovėliuose. Visi matematikos objektai yra abstraktūs. Pirmoji pažintis su abstrakcija turėtų būti gerai apgalvota. Teisybės dėlei reikia pripažinti, kad didaktikos žinių reikia ir matematikos dėstytojams. Toks neapdairumas yra kita prasta tradicija.
Mano nuomone, motyvacijos mokytis matematikos išsaugojimas ir skatinimas turi būti grindžiamas samprotavimų naudojimu ir prasmės atskleidimu mokyklinėje matematikoje. Pavyzdžiais ar tyrimais pagrįsti tokį teiginį yra labai sunku. Paprasčiau tokį teiginį galima būtų bandyti pagrįsti matematikos ir jos mokymo istorijos apžvalga, bei pačios matematikos pažinimu. Nuorodų į tokio teiginio pagrindimą savo laiku esu pateikęs ne vieną (Matematinio ugdymo gairės). Šį kartą pacituosiu Amerikos matematikos mokytojų nacionalinę tarybą (matyt mūsų LMMA atitikmuo), kuri savo tekste Motivating Struggling Math Students rašo:
The NCTM recommends that math programs be based on developing and using reasoning and “sense making” skills. Reasoning is defined as beginning with ideas, proofs, etc. and, drawing conclusions about those ideas and proofs, based on evidence and/or assumptions. Sense making means that students understand math in context and are able to make connections between new learning and prior knowledge.
Seminaras Ukmergėje buvo bandymas aiškintis tokios rekomendacijos turinį. Tai bandymas aiškintis, ką matematikos mokytojas turėtų žinoti apie samprotavimų naudojimą ir prasmės atskleidimą aritmetikoje norėdamas sėkmingai ugdyti savo mokinių motyvaciją.
P.S. Pasirodo, tai yra 100-asis šio tinklaraščio įrašas.
P.P.S. Aš rašiau, kad ,,[m]otyvacija mokytis matematikos prarandama mokykloje palaipsniui, [m]otyvacijos praradimas turėtų būti juntamas tarp 6-7 klasės mokinių ir vėlesnėse klasėse tokių mokinių turėtų tik daugėti.” Tai patvirtina vienoje Vilniaus gimnazijoje atliktas tyrimas: R. Seniūnaitė ir B. Pociūtė. 10-16 metų mokinių nuostatos dėl matematikos ir metakognityvaus sąmoningumo sąsaja. Acta Paedagogica Vilnensia, 2015, 35. Viena iš straipsnio išvadų yra tokia: ,,…mokinių nuostata dėl matematikos mokymosi jiems tampant vyresniems yra mažiau pozityvi: pereidami iš pradinės mokyklos į vidurinę mokiniai turi labiau teigiamą nuostatą dėl matematikos negu pereidami iš vidurinės mokyklos į gimnaziją.” (citata iš 41 puslapio).