Kodėl neigiamųjų skaičių sandauga yra teigiamas skaičius?

School mathematics Add comments

Aug 092016

Kodėl dviejų neigiamųjų skaičių sandauga turėtų būti teigiamas skaičius? Galimų atsakymų į šį klausimą yra daug ir jie anaiptol nėra sudėtingi. Kita vertus, istorinės aplinkybės susiklostė taip, kad ši tema ilgą laiką buvo kontraversinė, bent jau Vakarų kultūroje. Tai parodau toliau remdamasis matematikos istorijos tekstais. Blogai yra tai, kad šis ir panašūs klausimai mokykloje yra pateikiami kaip akivaizdūs; kaip ,,taisyklės”, kurių dera laikytis ir tiek. Taip yra šiandieninėje mūsų mokykloje. Taip buvo ir anksčiau. Neigiamųjų skaičių sandaugos klausimą mini Stendalis 1836 metais vaizduodamas savo pažinties su matematika patirtį (The Life of Henry Brulard):

In my view, hypocrisy was impossible in mathematics and, in my youthful simplicity, I thought it must be so in all the sciences to which, as I had been told, they were applied. What a shock for me to discover that nobody could explain to me how it happened that: minus multiplied by minus equals plus. Not only did people not explain this difficulty to me (and it is surely explainable, since it leads to truth) but, what was much worse, they explained it on grounds which were evidently far from clear to themselves. […]

”But it’s the custom; everybody accepts this explanation. Why, Euler and Lagrange, who presumably were as good as you are, accepted it! […] It seems you want to draw attention to yourself.”

As for M. Dupuy, he treated my timid objections (timid because of his pompous way of speaking) with a haughty smile that verged on aloofness.

Prieš kreipdamasis į matematikos istorijos tekstus apžvelgiu keletą galimų atsakymų į pradinį klausimą.

Kodėl dviejų neigiamųjų skaičių sandauga turėtų būti teigiamas skaičius?

Kalbant apie teigiamuosius ir neigiamuosius skaičius bei jų aritmetiką septintoje klasėje pasakoma, kad ,,turime žinoti taisyklę” $(-1){\cdot}(-1) =1$ . Tačiau labai dažnai neišgirstame paaiškinimų kodėl matematikoje taikoma ši ,,taisyklė” ir koks jos statusas – tai aksioma ar teorema? Šiai temai skirtoje Ugdymo plėtotės centro platinamoje video-pamokoje keletą kartų pakartojoma: ,,paradoksalu, bet du blogiečiai padaro kažką gero”. Man neteko matyti kokių nors kitų paaiškinimų dabartiniuose mūsų vadovėliuose.

Gal būt šiek tiek geriau reikalai klostosi su sveikųjų skaičių sumos ir atimties apibrėžtimis. Kai kuriuose vadovėliuose šioms apibrėžtims motyvuoti pasitelkiami realaus pasaulio pavyzdžiai. Matematinis argumentas toms apibrėžtims yra noras, kad lygybė

$(a - x) + x = a$ (1)

būtų teisinga visiems sveikiesiems skaičiams $a, x$ , teigiamiems ir neigiamiems.

Grįžtant prie daugybos prisiminkime, kad natūraliųjų skaičių sandauga apibrėžiama kaip kartotinė sudėtis. Pavyzdžiui,

$3{\cdot}5 = 5 + 5 + 5 = 15$

Lygiai taip pat galėtume apibendrinti šį pavyzdį, kai vietoje 5 yra 0 arba -5. Būtent,

$3{\cdot}0 = 0 + 0 + 0 = 0\quad\mbox{ir}\quad 3{\cdot}(-5) = (-5) + (-5) + (-5) = - 15.$

Kaip apibendrinti tokią sandaugą, kai pirmasis dauginamasis yra neigiamas skaičius? Darydami prielaidą, kad neigiamųjų skaičių aritmetika turėtų turėti tas pačias savybes kaip ir teigiamųjų, naudosimės sandaugos perstatymo dėsniu (komutatyvumu). Būtent,

$0{\cdot}5 = 5{\cdot}0=0+0+0+0+0=0,$

$(-3){\cdot}5 = 5{\cdot}(-3)=(-3)+(-3)+(-3)+(-3)+(-3)=-15.$

Toliau aiškinsimės, kaip apibrėžti sandaugą $(-3){\cdot}(-5)$ ?

Iš to, kas pasakyta galima daryti dvi priešingas išvadas. Jei dauginant vieną neigiamą skaičių iš teigiamo skaičiaus gauname neigiamą skaičių, tai dauginant du neigiamus skaičius tuo labiau turėtume gauti neigiamą skaičių. Kita išvada gali remtis šia lenetele:

$3{\cdot}5=+15 \quad 3{\cdot}(-5)=-15$

$(-3){\cdot}5=-15 \quad (-3){\cdot}(-5)=?$

Lentelėje iš keturių sandaugų dvi yra neigiami skaičiai. Dėl ,,lygių galimybių” reikėtų, kad dvi kitos sandaugos būtų teigiami skaičiai. Vargu ar šie samprotavimai gali ką nors įtikinti. Toliau pateikiu keletą skirtingo matematinio giežtumo samprotavimų.

I aiškinimas Šios daugybos lentelės komentarai gali turėti daugiau prasmės už ankstesnės:

$3{\cdot}5=+15\quad\quad$ tris kartus gavus po 5 eurus viso turėsime 15 eurų;

$3{\cdot}(-5)=-15\quad$ tris kartus mokėdami 5 eurų baudą viso sumokėsime 15 eurų baudą;

$(-3){\cdot}5=-15\quad$ tris kartus negaudami po 5 eurus viso negausime 15 eurų;

$(-3){\cdot}(-5)=15$ tris kartus nemokėdami 5 eurų baudos viso išsaugosime 15 eurų.

II aiškinimas Šis aiškinimas grindžiamas intuityviai akivaizdžiu sąryšiu:

$\mbox{atstumas} = \mbox{greitis}\,{\cdot}\,\mbox{laikas}.$ (2)

Dydžiai šiame sąryšyje paprastai matuojami teigiamais skaičiais. Bet galima ir kitokia interpretacija. (2) sąryšyje įstatykime tokias, gal būt, neįprastas dydžių reikšmes:

$\mbox{greitis} =$ trys metrai per sekundę judant atgal, neigiamas skaičius;
$\mbox{laikas} =$ penkios sekundės į praeitį, neigiamas skaičius;
tokiu atveju, prieš penkias minutes, jūs buvote 15 metrų priekyje, t.y. $\mbox{atstumas} =$ 15 metrų.

Įstatę šias reikšmes į (2) sąryšį gauname

$(-3){\cdot}(-5)=15.$

III aiškinimas Šis aiškinimas remiasi prielaida, kad dauginimo rezultatas kinta tuo pačiu dydžiu kai vienas iš dauginamųjų kinta tuo pačiu dydžiu. Pradėkime nuo natūraliųjų skaičių sekos

$1,2,3,4,5,\dots$

Padauginę kiekvieną sekos narį iš 3 gauname naują seką:

$3,6,9,12,15,\dots$

Pratęskime abi sekas į kairę pusę išlaikydami tuos pačius skirtumus tarp gretimų sekos narių, t.y. iš kairiojo nario nuosekliai atimdami 1 ir 3, atitinkamai:

$\dots -5,-4,-3,-2,-1,0,1,2,3,4,5,\dots$

$\dots -15,-12,-9,-6,-3,0,3,6,9,12,15,\dots$

Gavome, kad pirmosios sekos narį -5 atitinka antrosios sekos narys -15. Tai yra motyvas apibrėžti sandaugą:

$3{\cdot}(-5)=-15.$

Ką šis motyvas siūlo dauginant neigiamus skaičius? Naudodami teigiamųjų ir neigiamųjų skaičių dauginimo rezultatą, padauginkime pradinę natūraliųjų skaičių seką iš -3:

$-3,-6,-9,-12,-15,\dots$

Dar kartą pratęskime pradinę ir pastarąją seką į kairę pusę išlaikydami tuos pačius skirtumus tarp gretimų sekos narių:

$\dots -5,-4,-3,-2,-1,0, 1,\quad 2,\quad 3,\quad 4,\quad 5,\dots$

$\dots 15,\,\,\, 12,\,\,\, 9,\,\,\, 6,\,\, 3,\,\, 0,-3,-6,-9,-12,-15,\dots$

Šį kartą gavome, kad pirmosios sekos narį -5 atitinka antrosios sekos narys 15. Todėl sandaugą iš -3 apibrėžiame taip:

$(-3){\cdot}(-5)=15.$

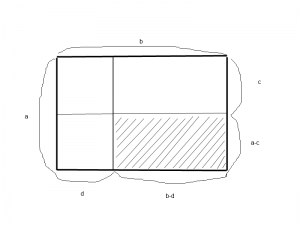
IV aiškinimas Skyrelį pradėjome primindami natūraliųjų skaičių sandaugos, kaip kartotinės sudėties, apibrėžimą. Skaičius tapatinant su skaičių spindulio taškais jų sandaugą galima apibrėžti kaip atitinkamo stačiakampio plotą. Neigiamųjų skaičių sandaugą taip pat galima gauti apibendrinant šį apibrėžimą.

Paveikslėlyje pavaizduoti keturi stačiakampiai su nurodytais kraštinių ilgiais. Užbrūkšniuoto stačiakampio plotą $(a-c){\cdot}(b-d)$ galima susieti su didžiojo stačiakampio plotu $a{\cdot}b$ formule:

$(a-c){\cdot}(b-d)=a{\cdot}b-d{\cdot}a-c{\cdot}b+d{\cdot}c,$ (3)

kurioje $a, b, c, d$ yra natūralieji skaičiai, $c<a$ ir $d<b.$ Pastarosios dvi nelygybės atsiranda dėl to, kad $a-c$ ir $b-d$ yra atkarpų ilgiai. Dabar pamirškime kaip gavome (3) formulę ir tarkime, kad ji teisinga kai $a, b, c, d$ yra bet kokie sveikieji skaičiai. Imkime $a=b=0$ , $c=3,$ $d=5$ ir darykime prielaidą, kad daugindami iš nulio gauname nulį. Įstatę šias reikšmes į (3) formulę gauname

$(-3){\cdot}(-5)=15.$

Šis apibendrinimas panašus į sumos ir atimties apibendrinimą išsaugant (1) sąryšį.

V aiškinimas Šis aiškinimas remiasi prielaida, kad teigiamųjų ir neigiamųjų skaičių aritmetika turi tas pačias savybes.

1 teiginys. Tarkime, kad sveikųjų skaičių aibėje Z galioja sumos perstatymo (komutatyvumo) bei jungimo (asociatyvumo) dėsniai, skirstymo dėsniai (distributyvumas), o lygybės $z+(-z)=0$ , $z+0=z$ , $0{\cdot}z=z{\cdot}0=0$ ir $1{\cdot}z=z$ teisingos kiekvienam $z\in$ Z. Tada $3{\cdot}(-5)=-15.$

Įrodymas. Naudodami skirstymo dėsnį ir tai, kad $5+(-5)=0$ gauname

$15+ 3{\cdot}(-5)=3{\cdot}5+3{\cdot}(-5)=3{\cdot}(5+(-5))=3{\cdot}0=0.$ (4)

Naudodami lygybę $z+0=z$ kai $z=3{\cdot}(-15)$ ir $z=-15$ , bei lygybę $0=15+(-15)$ , gauname

$3{\cdot}(-5) = 3{\cdot}(-5)+0 = 3{\cdot}(-5)+(15+(-15))$

sumos jungimo dėsnis $= (3{\cdot}(-5)+15)+(-15)$

sumos perstatymo dėsnis $= (15 + 3{\cdot}(-5))+(-15)$

dėl $(4) = 0+(-15)$

sumos perstatymo dėsnis $= (-15)+0 = -15,$

ką ir reikėjo įrodyti.

2 teiginys. Tarkime, kad teisingos 1 teiginio prielaidos. Tada $(-3){\cdot}(-5)=15.$

Įrodymas. Naudodami lygybę $z+0=z$ kai $z=(-3){\cdot}(-15)$ ir $z=15$ , bei lygybę $0=(-z)+z=z+(-z)$ kai $z=15$ ir $z=3$ , gauname

$(-3){\cdot}(-5) = (-3){\cdot}(-5) +0=(-3){\cdot}(-5) +((-15)+15)$

sumos jungimo dėsnis $= ((-3){\cdot}(-5)+(-15))+15$

dėl 1 teiginio $= ((-3){\cdot}(-5)+3{\cdot}(-5))+15$

skirstymo dėsnis $= ((-3)+3){\cdot}(-5)+15$

$=0{\cdot}(-5)+15 = 0+15 = 15,$

ką ir reikėjo įrodyti.

VI aiškinimas Šiame aiškinime darome prielaidą, kad skaičius yra geometrinės tiesės taškas. Pasirinkę tiesėje bet kuriuos du taškus ir pavadinę juos 0 ir 1, galime joje atidėti bet kuriuos kitus natūraliuosius skaičius. Šią tiesę vadinsime skaičių tiese. Sakysime, kad nelygaus nuliui skaičių tiesės taško $p$ veidrodinis atvaizdis atžvilgiu nulio yra toks taškas $p^{\ast}$ , kad $p^{\ast\ast}:=(p^{\ast})^{\ast} = p$ . Nulio veidrodinį atvaizdį vadinsime jį patį, t.y. $0^{\ast}:=0$ . Neigiamais skaičiais pavadinsime natūraliųjų skaičių veidrodinius atvaizdžius, t.y. $-n := n^{\ast}$ su kiekvienu $n\in$ N.

Kaip ir ankstesniame aiškinime, darydami prielaidą, kad sveikųjų skaičių aibėje yra apibrėžtos sumos ir sandaugos operacijos turinčios įprastines savybes, įrodysime, kad bet kurio skaičiaus sandauga iš $1^{\ast}$ yra jo atvirkštinis atvaizdis, t.y. su kiekvienu sveikuoju skaičiumi $m$ teisinga lygybė

$1^{\ast}{\cdot} m = m^{\ast}.$ (5)

Kai ši lygybė bus paaiškinta (įrodyta), tai, imdami $m=1^{\ast}$ , gausime norimą lygybę

$(-1){\cdot}(-1)=1^{\ast}{\cdot}1^{\ast}=1^{\ast\ast}=1.$

3 teiginys Tarkime, kad teisingos 1 teiginio prielaidos. Tada bet kuriems sveikiesiems skaičiams $x$ ir $y$ teisinga implikacija

jei $x+y=0,$ tai $x=y^{\ast}.$

Įrodymas Tarkime, kad $x+y=0$ . Naudodami sumos savybes gauname lygybes

$x=x+0=x+(y+y^{\ast})=(x+y)+y^{\ast}$

(dėl prielaidos $x{+}y=0$ ) $=0+y^{\ast}=y^{\ast}+0=y^{\ast}.$

Teiginys teisingas remiantis implikacijos teisingumo lentele.

Dabar jau galime paaiškinti (5).

4 teiginys Tarkime, kad teisingos 1 teiginio prielaidos. Tegul $m$ yra sveikasis skaičius. Tada teisinga (5) lygybė.

Įrodymas Pakanka įrodyti, kad $1^{\ast}{\cdot}m + m=0$ . Iš tikro, (5) lygybė yra šio fakto, 3 teiginio su $x=1^{\ast}{\cdot}m$ ir $y=m$ , bei modus ponens išvada. Kadangi $1{\cdot}m=m$ , tai

$1^{\ast}{\cdot}m+m=1^{\ast}{\cdot}m+1{\cdot}m$

(skirstymo dėsnis) $=(1^{\ast}+1){\cdot}m=0{\cdot}m=0,$

ką ir reikėjo įrodyti.

Neigiamųjų skaičių sampratos evoliucijos fragmentai

Iki 19 amžiaus pabaigos Europos matematikoje neigiamieji skaičiai nebuvo pilnai pripažinta aritmetikos dalimi. Tuo tarpu Kinijoje ir Indijoje gerokai anksčiau neigiamieji ir teigiamieji skaičiais buvo laikomi iš esmės lygiaverčiais. Šia prasme neigiamųjų skaičių istorija yra ypatinga, nors ne vienintelė tokia. Glaustą savąjį šios istorijos variantą siūlo D. Mumfordas straipsnyje What’s so Baffling About Negative Numbers? – a Cross-Cultural Comparison. Juo autorius pagrindžia dvi priežastis paaiškinančias neigiamųjų skaičių kontraversiją Vakarų kultūros kontekste. Pirma, iki 17 amžiaus Euklido ,,Pradmenys” turėjo didžiulę įtaką matematikos vystymosi krypčiai ir jos supratimui. Skaičiaus ir dydžio samprata šiame Euklido veikale nepalieka vietos neigiamiesiems skaičiams. Antra, atsitiko taip, kad kartu su neigiamaisiaisskaičiais prisireikė menamųjų skaičių (kvadratinės šaknys iš neigiamų skaičių). Kadangi pastarieji kėlė ypatingą įtarimą, tai tik didino nepasitikėjimą neigiamaisiais skaičiais.

Neigiamieji skaičiai Rytų kultūros matematikoje Jiuzhang Suanshu (Nine Chapters on the Mathematical Art) yra kinų matematikos knyga savo svarba panaši į Euklido ,,Pradmenis” Vakarų kultūroje. Knygą sudaro matematikos sąvokos ir metodai, kurie atsirado palaipsniui, pradedant Zhou (ar Chou) dinastija (1000 m. pr. Kr.) ir toliau plėtojami Vakarų Han dinastijoje (iki 9 amžiaus). Skirtingai nuo Euklido samprotaujamosios matematikos, kinų Devyniuose Skyriuose randami tik praktiniai realaus pasaulio uždaviniai ir jų sprendimo algoritmai, be jokių įrodymo užuominų. Devyni Skyriai išgyveno ilgą ir sudėtingą perrašinėjimų, naikinimo ir atkūrimo istoriją.

Savo laiku pirmajame tūkstantmetyje prieš mūsų erą kiniečiai pradėjo naudoti skaičiavimo lazdeles, grupuodami jas eilėmis ir naudodami dešimtainę sistemą. Atlikdami skaičiavimus, skirtingus skaičius reiškė lazdelių eilėmis, kurios sudarė groteles.

Neigiamieji skaičiai Devyniuose Skyriuose naudojami sprendžiant tiesines lygtis. Lygčių sprendimo metodas yra tas pats, kurį mes dabar vadiname Gauso nuoseklaus nežinomųjųeliminavimo metodu. Teigiamieji skaičiai vaizduojami raudonomis lazdelėmis, o neigiami skaičiai – juodomis. Mumfordo teigimu, iš knygos teksto darosi aišku, kad neigiamieji skaičiai buvo nagrinėjami ir naudojami visiškai teisingai tada, kai jųprisireikdavo, galimai pirmą kartą pasaulyje. Kai kuriuose Devynių Skyrių variantuose randamos tiesiogiai suformuluotos teigiamųjų ir neigiamųjų skaičių dauginimo taisyklės.

Kinų algebra suklestėjo Songo ir Yuano dinastijose. Kinų matematikas Zhu Shijie (apie 1260 – apie 1320) ištobulino Gauso metodą taikydamas jį sprendžiant daugianarių sudarytoms lygčių sistemoms. Neigiamųjų skaičių teorijos žinojimas yra būtina sąlyga plėtojant algebrą. Zhu algebra pasiekė tokį lygį, kuris Europoje nebuvo pasiektas iki 19 amžiaus pabaigos.

Tuo tarpu Indijoje neigiamieji skaičiai akivaizdžiai naudojami dar 628 mūsų eros metais pasirodžiusiame Brahmaguptos veikale Brahma-sphuta-siddhanta. Manoma, kad ankstesniuose indų darbuose skirtuose finansiniams skaičiavimams neigiami skaičiai turėjo turėti prasmę bent jau netiesiogiai. Brahmaguptos veikale daugiau dėmesio skiriama astronomijai (saulės, mėnulio ir planetų judėjimo ir jų padėties duotu momentu nustatymas). Didelė teksto dalis turi eilėračių formą, turinys perteikiamas labai koncentruotai ir yra sunkiai suprantamas, žinios skirtos mokytis mintinai perduodant jas iš kartos į kartą. Matematikai skirti du knygos skyriai ir ją sudaro ankstesniai laikais sukauptos matematikos sąvokos ir metodai. Teigiamųjų ir neigiamųjų skaičių aritmetika yra aiškiai suformuluota eilėraščių formoje. Mumfordas išreiškia gailestį, kad nėra jokių duomenų paaiškinančių kaip buvo gauti, mūsų požiūriu, visiškai teisingi neigiamųjų skaičių aritmetikos teiginiai. Matyt tai yra Vedų tradicijos žinias perduoti žodžiu pasekmė.

Kaip ir Kinijoje, indų žinios apie neigiamuosius skaičius leido jiems gilintis į algebrą. Žinių gilumą rodo jų gebėjimas spręsti kai kurias sudėtingas lygtis ir suprasti jų sprendinių savybes. Tačiau indų mokslininkai matematika domėjosi ne dėl jos pačios, bet dėl jos reikalingumo prognozuojant saulės, mėnulio ir planet judėjimą.

Įdomu tai, kad skaičių žymėjimas taškais geometrinėje tiesėje į dešinę nuo nulio atidedantteigiamus skaičius ir į kairę nuo nulio atidedant neigiamus skaičius naudojamas 12-ame amžiuje Bhaskara II darbuose. Europoje tokia idėja gimė tik 17 amžiaus pabaigoje Walliso darbuose (Descartesas taškais koordinačių ašyse žymėjo tik teigiamus skaičius).

Al-Khwarizmi ir neigiamieji skaičiai Standartinė matematikos istorija sako, kad viduramžiais arabai buvo tarpininkais, kurių dėka europiečiai atgavo Antikinės Graikijos matematikų palikimą, o kartu su juo sužinojo apie indų ir arabų matematikų darbus. Tačiau, bent jau indų požiūris į neigiamuosius skaičius šiuo keliu į Europą nepateko. Kaip tai galėjo atsitikti?

Manoma, kad Europoje apie arabų matematikos žinias sužinota 12-ame amžiuje, kai į lotynų kalbą buvo išversti persų matematiko Al-Khwarizmi (apie 780 – apie 830) darbai. Svarbiausias jų yra kvadratinių lygčių sprendimui skirtas veikalas The Compendious Book on Calculation by Completion and Balancing. Pavadinimo lotyniškame vertime pasirodė žodis, kuris evoliucionavo į matematikos terminą ,,algebra”. Knygoje parodoma kaip bet kurią pirmojo ir antrojo laipsnio lygtį suvesti į vieną iš šešių bendro pavidalo lygčių. Tiesa, knygoje nėra naudojami matematiniai simboliai įprasti dabartinėje matematikoje. Tokia algebros forma vadinama retorine. Bet samprotavimai yra panašūs į šiais laikais įprastus lygčių pertvarkymus. Šie pertvarkymai buvo naujas metodas skirtingas nuo Euklido ,,Pradmenyse” naudojamo geometrinio įrodymo metodo. Naujasis metodas pradėtas vadinti simboliniu mąstymu.

Al-Khwarizmi knygoje apie algebrą Mumfordas išskiria tris jo teigimu ypatingai keistus dalykus. Pirma, neigiamieji skaičiai sutinkami tik vieną kartą, kai bandoma pagrįsti (3) lygybę. Bet kitose vietose neigiami skaičiai daugiau neminimi. Antra, nagrinėjamos kvadratinės lygtys turi tik teigiamus koeficientus ir todėl yra vieno iš trijų tipų:

$ax^2+bx=c$ , $a, b, c>0$ ;
$ax^2+c=bx$ , $a, b, c>0$ ;
$ax^2=bx+c$ , $a, b, c>0$ .

Lygybė šiose lygtyse reiškia lygybę tarp teigiamų skaičių. Tokia kvadratinių lygčių kvalifikacija yra būdingai beveik visai europinei tradicijai iki 19 amžiaus vidurio. Trečia, Al-Khwarizmi nagrinėjo vieną Bhaskara II užduotį, išskyrus tuos jos atvejus, kuriuose pasirodo neigiamieji skaičiai.

Kol kas galime tik spėlioti kodėl Al-Khwarizmi vengė neigiamųjų skaičių. Gal būt Euklido ,,Pradmenys” jam padarė tą pačią įtaką kaip ir daugumai Europos matematikų kaip matysime toliau.

Abacus rankraščiai Pirmasis Europos matematikoje žinomas neigiamųjų skaičių dauginimo taisyklės aiškinimas rastas 1344 metų abacus rankraštyje Aliabraa argibra, kurio autorius yra Dardi iš Pizos. Šis aiškinimas kodėl sudauginus neigiamuosius skaičius gauname teigiamą skaičių, jo žodžiais tariant less times less makes plus, atrodo taip (cituoju iš J. Høyrup. Hesitating progress – the slow development toward algebraic symbolism in abacus-and related manuscripts, c. 1300 to c. 1550. In A. Heefer and M. Van Dyck (eds.) Philosophical Aspects of Symbolic Reasoning in Early Modern Mathematics, Studies in Logic, vol. 26, 2010, 23 pusl.):

Now I want to demonstrate by number how less times less makes plus, so that every times you have in a construction to multiply less times less you see with certainty that it makes plus, of which I shall give you an obvious example. 8 times 8 makes 64, and this 8 is 2 less than 10, and to multiply by the other 8, which is still 2 less than 10, it should similarly make 64. This is the proof. Multiply 10 by 10, it makes 100, and 10 times 2 less makes 20 less, and the other 10 times 2 less makes 40 less, which 40 less detract from 100, and there remains 60. Now it is left for the completion of the multiplication to multiply 2 less times 2 less, it amounts to 4 plus, which 4 plus join above 60, it amounts to 64. And if 2 less times two less had been 4 less, this 4 less should have been detracted from 60, and 56 would remain, and thus it would appear that 10 less 2 times 10 less two had been 56, which is not true. And so also if 2 less times 2 less had been nothing, then the multiplication of 10 less 2 times 10 less 2 would come to be 60, which is still false. Hence less times less by necessity comes to be plus.

Prieš tai Dardi smulkmeniškai formuluoja dvinarių dauginimo taisyklę. Tai yra retorinės algebros pavyzdys, kai dar nebuvo naudojami dabar įprasti žymėjimai ir formulės. Dabar jo samprotavimą išreikštume keliomis eilutėmis: kadangi $8^2=64$ ir $8=10-2$ , tai

$64=(10-2){\cdot}(10-2)=100+2{\cdot}(-2){\cdot}10 +(-2){\cdot}(-2)$

Kadangi sandauga $(-2){\cdot}10=-20$ abejonių nekelia, pastaroji lygybė teisinga tik tuo atveju, kai $(-2){\cdot}(-2)=4$ . Toks aiškinimas aptinkamas daugelyje vėlesnių abacus rankračių pasirodžiusių 15 amžiuje. Kas tie abacus rankraščiai?

Abacus rankraščiai yra tekstai, kurie buvo naudojami Italijoje nuo maždaug 1280 metų iki maždaug 1550 metų mokyti 11-12 metų vaikus praktinės matematikos; jie buvo ruošimo komercinei veiklai dalimi. Bendrais bruožais abacus rankraščių turiniai panašūs. Paprastai pradedama nuo indų-arabų skaičiavimo sistemos įvedimo ir tęsiama prekybai aktualių užduočių sprendimais. Nors yra ir užduočių, kurias reikėtų vadinti ,,teorinėmis” ir pramoginėmis. Loginiais samprotavimais pagrįstų įrodymų \emph{abacus} rankraščiuose nėra. Tačiau naudojamos kai kurios skaičiavimo tikslumo tikrinimo taisyklės. Pavyzdžiui, dalybos iš 7 taisyklės naudojimas patikrinti ar teisingai suskaičiuota sandauga $341{\cdot}625 = 213125$ atrodo taip: dalindami 341/7 gauname liekaną 5, dalindami 625/7 gauname liekaną 2, po to sudauginę liekanas $2{\cdot}5=10$ ir dalindami 10/7 gauname liekaną 3; ši liekana turi sutapti su liekana gauta dalinant 213125/7. Be to, naudojamos standartinėmis laikomos skaičiavimos taisyklės. Pavyzdžiui, vadinamoji rule of three reiškė implikaciją

$\mbox{jei}\quad AB :: CD\quad\mbox{tai}\quad AD = BC.$

Daugiau komentarų yra K. Neal knygos From discrete to continuous : the broadening of number concepts in early modern England 3.1 skyriuje.

Abacus rankraščių rašymas ir studijos būdingos ne tik Italijai. Šiek tiek vėliau ši tradicija išplito po visą Europą. Labai dažnai šių rankraščių pavadinimuose naudojamas žodis ,,aritmetika”. Kai kurie rankraščiai turėjo net spausdintą formą. Šie leidiniai buvo vieninteliai komercinės aritmetikos žinių šaltiniai iki 16 amžiaus. Pavyzdžiui, 1568 metais Anglijoje Hunfrey Baker publikavo knygą pavadintą Well-Spring of Science, kurios paantraštė Teaching the Perfect Worke and Practice of Arithmetick, both in Numbers and Fractions.

Atrodo, kad abacus rankraščių reikšmė matematikos istorijoje nėra aiški ir vienareikšmė. Sprendžiant pagal minėtąjį J. Høyrupo straipsnį, abacus rankraščių turinyje galima įžvelgti du sluoksnius: vienas perimtas iš Leonardo Pisano (arba Fibonacci) knygos Liber abaci (1202/1228), o kitas sluoksnis nepriklausomas, lyg ir savarankiškas. Be to, tai, kas perimta iš Leonardo Pisano, abacus rankraščiuose yra nesuprasta. Neabejotinai abacus rankraščių matematiką įtakojo arabų algebra. Bet kokiu būdu ir kokiu mastu neaišku. Kita vertus Mumfordas teigia, kad aritmetinės operacijos ir taisyklės knygos Liber abaci pirmojoje dalyje nagrinėja tik natūraliuosius skaičius ir teigiamas trupmenas. Neigiami skaičiai pasirodo labai epizodiškai tik antroje knygos dalyje sprendžiant ,,žodinius” uždavinius ir nuolat rūpinantis juos tinkamai interpretuoti.

Galima spėti, kad neigiamieji skaičiai nekėlė esminių problemų naudojant matematiką praktinėje veikloje. Kitaip atrodė tiems, kurie matematiką suvokė per Euklido ,,Pagrindus”. Šiuo požiūriu Mumfordas apžvelgė ne tik Leonardo Pisano darbą, bet ir Nicole Oresme (1323-1382), Luca Pacioli (1445-1517), Girolamo Cardano (1501-1576), Galileo (1565-1642), Fermat (1601-1665), pastebėdamas, kad tai tik maža dalis tų, kurių darbai neigiamųjų skaičių požiūriu galėtų būti apibūdinti panašiai. \emph{Mumford}o nuomone, požiūrį į neigiamuosius skaičius pradėjo keisti Wallisas ir Newtonas. Prieš sakant kažką konkrečiau apie Wallisą manau reikalinga aptarti ir konkretų argumentą nukreiptą prieš įprastąją neigiamųjų skaičių sandaugos taisyklę.

Arnauldo paradoksas Prancūzas Antoine Arnauldas (1612-1694) atkreipė dėmesį į neigiamųjų skaičių daugybos taisyklės prieštaringumą proporcijų teorijos kontekste. Diskusijoje su kitu prancūzu Jeanu Prestetu (1648-1691) A. Arnauldas rašė:

It is for this reason that I cannot understand that the square of -5 can be the same thing as the square of +5, and that both of them are +25. Moreover, I do not know how to fit this with the fundamental property of multiplication, that is that the unity is to one of the magnitudes that are multiplied as the other is to product. Which thing is true of the integers and of the fractions as well. For 1 is to 3 as 4 is to 12 … But I cannot fit this to the multiplications of two minuses. For shall one say that +1 is to -4 as -5 to +20? I do not see this. For +1 is greater than -4. On the contrary -5 is less that +20. Whereas in all the other proportions if the first term is greater than the second then the third must be greater than the fourth.

(Čia ir toliau cituoju iš Gerto Schubringo knygos Conflicts Between Generalization, Rigor, and Intuition. 2005) Apie kokią fundamentaliąją sandaugos savybę čia kalbama ir kuo ji netinka neigiamiesiems skaičiams? Manau, kad kalbama apie savybę, kuri išplaukia iš Euklido ,,Pradmenų” 5 knygos faktų. Tarkime $n$, $m$ ir $k$ yra natūralieji skaičiai. Elgdamiesi su natūraliaisiais skaičiais kaip su Antikinės matematikos dydžiais ir naudodami ,,Pradmenų” 5 knygos teiginius V.7, V.11 ir V.15, galime tvirtinti, kad nurodyti trys teiginiai yra ekvivalentūs:

$nm=k\Leftrightarrow m:nm :: m: k\Leftrightarrow 1:n :: m: k .$ (5)

Iš esmės tai yra “rule of three” naudota dar senovės Indijoje. Mūsų mokykliniuose vadovėliuose tai pagrindinė proporcijos savybė. Pritaikęs (5) faktus neigiamųjų skaičių sandaugai, Arnauldas gauna

$(-4){\cdot}(-5)=+20\Leftrightarrow+1 : -4 :: -5 : +20.$

Toliau Arnauldas samprotauja taip. Kadangi $+1 > -4$ ir santykis $+1 : -4$ yra proporcingas santykiui $-5 : +20$ , tai $-5 > +20$ – nesąmonė. Šis teiginys išplaukia iš santykio apibrėžties Euklido ,,Pradmenyse”. Tada Arnauldas daro išvadą, kad neigiamųjų skaičių sandauga negali būti teigiamu skaičiumi. Jo argumentas yra žinomas kaip Arnauldo paradoksas.

Arnauldo argumentas rodo, jog ne visos natūraliųjų skaičių savybės akivaizdžiai apibendrinamos neigiamiesiems skaičiams. Natūraliesiems skaičiams $n$ santykis tarp $n+1$ ir $n-1$ yra didesnis už santykį tarp $n-1$ ir $n+1$ . Tačiau šis sąryšis tarp santykių apsiverčia jei vietoje $n$ imsime neigiamuosius skaičius ir jei neigiamųjų skaičių sandauga yra teigiamas skaičius. Arnauldo paradoksas padarė nemažą įtaką vėlesnėse diskusijose apie neigiamuosius skaičius. Arnauldo paradokso atsiradimo aplinkybės taip pat įdomios.

Antoine Arnauldas buvo Romos katalikų teologas, filosofas bei matematikas. Mokėsi Sorbonoje Paryžiuje kol jėzuitai jo iš ten neišvarė. Nuo tada jis gyveno netoli Paryžiaus esančiame Port-Royalio vienuolyne. Arnauldas buvo svarbiu partneriu Descartesui dialoge apie pažinimo metodą. Be to, padarė nemažą matematinę įtaką Leibnizui, kai šis buvo apsistojęs Paryžiuje. Arnauldas kartu su P. Nicole 1662 metais parašė tarp filosofų gerai žinomą veikalą Logic of Port-Royal. Kartu su kitais Port-Royalio nariais Arnauldas buvo vienu iš Jansenizmo atstovu Prancūzijoje. Jėzuitų dėka 1679 metais Arnauldas buvo ištremtas į Nyderlandus ir Flandriją.

Kontraversijai dėl neigiamųjų skaičių turėjęs įtaką paradoksas atsirado Arnauldui tobulinant geometrijos vadovėlius. 1667 metais pasirodęs Arnauldo vadovėlis Nouveaux Élémens de Géométrie radikaliai pakeitė Euklido ,,Pradmenų” metodologinę struktūrą: pirmos keturios knygos skirtos veiksmų su dydžiais pagrindams ir tik po to sekė šių bendrų rezultatų taikymas geometrijai. Be to, vadovėlyje pradėti naudoti nauji algebriniai metodai. Vadovėlio autorius teigė, jog dydžius žymint raidėmis nebereikia rūpintis raidės prasme, kadangi svarbūs tik santykiai tarp jų.

Besides, he added, it was one of his book’s particular advantages that ir trained the mind to understand things in a “spiritual manner,” without the help of any “sensible” images.

rašoma G. Schubringo knygos 51 pusl. Tai buvo pirmasis naujo stiliaus universitetinis vadovėlis, kuris skyrėsi nuo Euklido iš esmės. Tačiau viena naujojo vadovėlio savybė neprigijo – jame nebuvo nurodytas autorius.

Dar vienas keistas \emph{Arnauld}o vadovėlio komentaras liečia neigiamųjų skaičių sandaugos taisyklę (pagal Schubringą 52 pul.):

MINUS by minus gives plus: that is to say that the multiplication of two terms, both of which have the sign minus, gives a product which must have the sign plus. […] This appears rather strange, and in fact it cannot be imagined that this could happen other than by accident. For of themselves, minus multiplied by minus can only give minus.

Taip, čia apgailestaujama, kad taisyklė prieštarauja tam, kas iš tikro turėtų būti: minusų sandauga yra minusas. Daugiau komentarų šia tema vadovėlyje nėra. Bet po vadovėlio pasirodymo vyko diskusija laiškais tarp Arnauldo ir Presteto, kurią pastarasis 1675 metais publikavo savajame vadovėlyje Elémens des Mathématiques. Ten ir yra suformuluotas Arnauldo paradoksas.

Apie Presteto vadovėlį 53 puslapyje Schubringas rašo taip:

Prestet’s textbook indeed contains the first account of negative numbers in which the negatyve numbers are presented as having the same status as positive numbers, and in which the rule of signs is “proved” not geometrically, but algebraically.

Tvirtinimas dėl prioriteto vargu ar pagrįstas. Reikėtų palyginti Presteto vadovėlio turinį su anksčiau minėtu Dardi abacus rankraščiu. Panašų pirmumo teiginį Mumfordas priskiria Walliso knygai (ibid, 137 pusl.), apie kurią rašau toliau.

Wallisas ir neigianieji skaičiai Mumfordo nuomone (ibid, 136 pusl.), Johnas Wallisas (1616-1703) ir Isaacas Newtonas (1642-1726/7) yra pirmieji Europos matematikai, kurių požiūriai į neigiamuosius skaičius panašūs į šiuolaikinį, t.y. šie skaičiai laikomi lygiaverčiais teigiamiesiems skaičiams. Tačiau, knygos From Discrete to Continuous autorės Katherine Neal vertinimas nėra toks vienareikšmiškas dėl neigiamųjų ir teigiamųjų skaičių lygiavertiškumo Walliso darbuose. Tai eilinį kartą rodo matematikos istorijos kaip tyrimų srities sudėtingumą.

Kaip ten bebūtų su vertinimais, galima šiek tiek remtis citatomis. 1685 metais publikuotoje Walliso knygoje A Treatise on Algebra rašoma (čia Specious yra Vietes terminas reiškiantis aritmetiką, kurioje naudojami raidėmis žymimi kintamieji):

To these Notes, Symbols or Species are prefixed (as occasion requires) not only numeral figures, but the signs + and – (or plus and minus), the former of which is a Note of Position, Affirmation or Addition; the other of Defect, Negation or Subduction: According as such Magnitude is supposed to be, or to be wanting. And where no such Sign is, it is presumed to be Affirmative and the sign + is understood.

And accordingly these Signs are still to be interpreted as in a contrary signification. If + signify Upward, Forward, Gain, Increase, Above, Before, Addition, etc. then – is to be interpreted of Downward, Backward, Loss, Decrease, Below, Behind, Subduction, etc. And if + be understood of these, then – is to be interpreted of the contrary.

(cituojama iš Walliso knygos 16 skyriaus Addition, Subdaction, Multiplication and Extraction of Roots in Specious Arithmetic ) Taip suprantamiems teigiamiesiems ir neigiamiesiems skaičiams siūlomas sandaugos pagrindimas:

For the true notion of Multiplication is this, to put the Multiplicand, or thing Multiplied (whatever it be) so often as are the Units in the Multiplier. . . . and this, whatever the thing Multiplied, Positive or Negative: for there may well be a Double Deficit as a Double Magnitude; and −2A is as much the Double of –A as +2A is the Double of A. . . .

But in case the Multiplier be a Deficit or Negative quantity; suppose −1; then instead of Putting the Multiplicand so many times, it will signify so many times to Take away the Multiplicand. . . . so that + by – makes –; But to Multiply –A by −2 is twice to take away a Defect or Negative. Now to take away a Defect is the same as to supply it; and twice to take away the Defect of A is the same as twice to add A or to put 2A . . . : So that – by – (as well as + by +) makes +.

Šį pagrindimą galima palyginti su I aiškinimu įrašo pradžioje. Toliau, rašydamas apie kvadratinių lygčių sprendimą, Wallisas atsisako jų klasifikavimo kaip pas Al-Khwarizmi ir naudoja vieną bendrą formą:

$\mbox{lygties}\quad x^2\pm 2bx\,=\,\pm c^2$

$\mbox{sprendiniais yra}\quad x\pm b\,=\,\sqrt{\pm c^2+b^2}.$

Tačiau rašydamas narius homogeninėje formoje (lygtyje vien tik kvadratiniai nariai), Wallisas šioje vietoje neatsisako Euklido stiliaus pagal kurį lygybė sieja plotus.

Yet is it not that Supposition (of Negative Quantities) either Unuseful or Absurd when rightly understood. And though, as to the bare Algebraick Notation, it import a Quantity less than nothing: Yet, when it comes to a Physical Application, it denotes as Real a Quantity as if the Sign were +; but to be interpreted in a contrary sense.

As for instance: Supposing a man to have advanced or moved forward (from A to B) 5 yards; and then to retreat (from B to C) 2 yards; If it be asked, how much had he Advanced (upon the whole march) when at C? I find . . . he has Advanced 3 Yards. But if, having Advanced 5 Yards to B, he thence retreat 8 Yards to D; and it then be asked, How much is he Advanced when at D, or how much Forwarder than when he was at A: I say –3 Yards. . . . That is to say, he is advanced 3 Yards less than nothing. . . . (Which) is but what we should say (in ordinary form of Speech), he is Retreated 3 Yards; or he wants 3 Yards of being so Forward as he was at A.

Wallisas ne tik vienodai vertino teigiamuosius ir neigiamuosius skaičius, jei pasikliauti Mumfordo vertinimu. Neal teigimu, Wallisas pirmasis tarp Europos matematikų pradėjo teikti aritmetikai pirmumą atžvilgiu geometrijos, kuri dominavo matematikoje nuo Antikos laikų.

Kaip jau minėjau, kontraversijos dėl neigiamųjų skaičių viena iš priežasčių Mumfordas laiko Euklido ,,Pradmenų” įtakingumą, o ne visos Antikos matematikos pasekme. Jis atkreipia dėmesį į kai kuriuos Antikos laikais žinomus matematikos faktus nepatekusius į Euklido ,,Pagrindus”. Cituoju Mumfordą (ibid, 141-142 pusl):

All in all, if you are going to start with Euclid, you are not going to be predisposed to introduce negative numbers in to your calculations. He has gone to extraordinary lengths to reduce arithmetic and algebra to geometry and thoroughly inoculate it against negatives. It is worth looking briefly at what else was known at 300 BCE which Euclid did not put in his book. There is apparently an unbroken tradition starting in Babylon in 1800 BCE and continuing through Ptolemy of calculating with the sexagesimal equivalent of decimals and approximating e.g. $\sqrt{2}$ and $\pi$ to many sexagesimal places. Moreover, there was also a tradition also going this far back of solving quadratic equations by algorithms – described in words but exactly equivalent to the quadratic formula. Euclid, in other words, distanced himself from a rich numerical tradition and consciously, it would seem, purified his version of mathematics.

The Europeans, then, had the benefit of this shining example of pure math and of the wonderful deductive logic on which they built. But it was hard to go beyond it in any radical way, to model other phenomena in the real world which cried out for negatives. Euclid was both the strength and the weakness of the European mathematical world of the 16th and 17th centuries.

Neigiamieji skaičiai 17-19 amžių matematikoje Įdomu yra tai, kad Walliso požiūrį į skaičius perėmė kontinentinės Europos matematikai, bet ne jo tėvynainiai. Ginčai dėl simbolių $-1$ ir $\sqrt{-1}$ prasmės įtakojo aritmetikos, geometrijos ir algebros evoliuciją, bei siejosi su matematikos prigimties aiškinimusi. Šis matematikos istorijos etapas Anglijoje nušviečiamas Helenos Pycior Symbols, Impossible Numbers, and Geometric Entanglements British Algebra through the Commentaries on Newton’s Universal Arithmetick knygoje, jos apimtis apie 340 puslapių. Knygos įvade rašoma: “[This book] also analyzes how, especially as the sought to legitimate the fertile negative and imaginary numbers, mathematicians began to undermine the existing mathematics, its rules and its standards”. Analogiškai istorijai Vokietijoje ir Prancūzijoje nušviesti Gertui Schubringui anksčiau minėtoje jo knygoje (Conflicts Between Generalizations, Rigor, and Intuition: Number Concepts Underlying the Development of Analysis in 17-19th Century France and Germany) prireikė apie 690 puslapių.

Pasak Mumfordo, 17-19 amžių Anglijoje neigiamieji skaičiai iš esmės buvo antrarūšiais matematikos objektais, fikcijomis ir panašiai. Pavyzdžiui, tokį požiūrį išreiškė 1843 metais Augustus De Morganas daugiatomės enciklopedijos Penny Cyclopaedia straipsnyje Negative and Impossible Quantities rašydamas:

It is not our intention to follow the earlier algebraists through their different uses of negative numbers. These creations of algebra retained their existence, in the face of the obvious deficiency of rational explanation which characterized every attempt at their theory.

Faktiškai visą De Morgano matematinių tyrimų kelią nulėmė neigiamieji skaičiai. Iš pradžių jis siekė surasti būdus, kaip sprendžiant lygtis, apsieiti be neigiamųjų skaičių naudojant tik teigiamuosius skaičius. Vėliau jo darbai evoliucionavo link abstrakčių algebrinių struktūrų kūrimo, kuriose neigiamieji skaičiai yra eiliniais elementais greta kitų skaičių. Kitaip tariant, neigiamieji ir teigiamieji skaičiai skaičių sistemoje tampa lygiateisiais elementais, priklausomais tik nuo struktūrą nusakančių dėsnių. Tokioje sistemoje neigiamųjų skaičių sandaugos taisyklė yra įrodoma išvada, panašiai kaip tai dariau V aiškinime. Iš esmės tai ir yra šiuolaikinės matematikos požiūris į neigiamuosius skaičius.

Grįžtant prie mokyklinės matematikos

Nors mokykloje mes išmokstame elgtis su neigiamaisiais skaičiais ir jie mums tampa įprastais, bet jų supratimas ir sampratos evoliucija lieka už mūsų ugdymo turinio ribų. Jau senokai mūsų matematikos mokytojų ir matematikos profesionalų rengimas tapo, švelniai kalbant, skurdžiu. Pavyzdžiui, Matematikos ir informatikos mokymo studijų programa apibūdinama taip:

Studijų programa skirta rengti aukštos kvalifikacijos mokytojus, galinčius mokyti matematikos ir informatikos (informacinių technologijų) dalykus bendrojo lavinimo mokyklose bei gimnazijose. Per ketverius studijų metus būsimieji pedagogai įgyja stiprius matematikos ir informacinių technologijų pagrindus, išmoksta ir taiko matematikos ir informatikos mokymo metodus, lavina bendravimo įgūdžius.

Čia ,,aukšta kvalifikacija” neapima gilaus elementariosios matematikos, matematikos istorijos ir matematikos filosofijos išmanymo. Tad nereikia stebėtis, kad mūsų mokyklinė matematika tapo taisyklių ir procedūrų rinkiniu. Kuo mūsų matematikos mokymas skiriasi nuo to kurį patyrė Stendalis 19 amžiaus pradžioje?

P.S. Amerikiečių nuomonė kaip ir ko turėtų mokytis būsimi matematikos mokytojai yra čia.

3 Responses to “Kodėl neigiamųjų skaičių sandauga yra teigiamas skaičius?”

Medardas says:

Tuesday August 9th, 2016 at 03:45 PM

Visus šiuos samprotavimus būtų galima sutrumpinti, jei pradžioje sutartume, kad neigiami skaičiai yra natūrinių skaičių sandauga su jų plėtiniu (-1), analogiškai, kaip kompleksinius skaičius gauname iš realių skaičių, kaip tiesinę kombinaciją su jų plėtiniu i=sqrt(-1) (t.y. i x i = -1), o hiperkompleksinius skaičius ir vektorinę algebrą apibrėžiame, kaip bazinio reperio (dar bendresnio plėtinio) tiesinį apvalkalą.
Natūrinių skaičių praplėtimo butinybė kyla iš empirinės logikos taisyklės – neiginio neigimas yra teigimas (trečiosios galimybės neigimo hipotezė klasikinėje logikoje) arba jo matematinio analogo – idempotento reikalavimo, kad P x P = 1. Analogiškai kitiems plėtiniams. Kaip teisingai pastebėta, praplėtimo būtinybė seka iš natūrinio skaičiaus sąvokos apibendrinimo, taip, kad sąvokoje nebeliktų ypatingų taškų – matematinių operacijų anomalijų, išimčių, nors nulio (ir begalybės) anomalija išlieka.
Tai yra šiuolaikinės matematikos pastangų algebraizuoti matematiką, t. y. tirti ne individualius matematinius dydžius, sąvokas, bet jų “kolektyvus”, “gentis”, “rūšis” – klases, aibes, kategorijas ir t. t., kaip generuojančių operacijų rezultatus. Algebra tradiciškai nagrinėja ne konkrečius dydžius bet, kaip pabrėžė Kurošas, tiria tuos dydžius apibrėžiančių operacijų savybes (nuo konkrečių skaičių formulėse pereiname prie jų abstrakcijų, vieningai žymimų raidėmis, ir įsivesdami plėtinius, vengdami “pavienių” išimčių). Už to slypi filosofijos pastanga rasti aukščiausio lygio abstrakciją ir visą matematiką pateikti, kaip hierarchinę tokių abstrakcijų piramidę. Analogiškai kitose mokslo šakose. Deja ši Hilberto iškelta matematikos formalizavimo programa žlugo, nes atvedė prie paradoksų ir antinomijų, kadangi pasirodė (Giodelio teorema), kad “aukščiausia” aksiomatinė abstrakcija būtinai yra atvira ir jai galima ir būtina (!) rasti plėtinius į meta abstrakciją. (Netrivialioje formalioje sistemoje yra neįrodomų ir nepaneigiamų tos formalios aksiomatinės sistemos rėmuose teiginių, t. y. tų teiginių prasmę lemia “išoriniai” šaltiniai). Iš analogijos su Euklido geometrija ir jos galimu nevienreikšmiu praplėtimu į neeuklidines (Rymano, Lobačevskio, topologines ir t.t.) geometrijas, galima tikėtis, kad tokie nepaneigiami ir/ar neįrodomi nagrinėjamos formalios sistemos teiginiai vienoje meta sistemoje gali būti teisingi, o kitoje, klaidingi arba vėl neapibrėžti ar net neturintys prasmių…
Viskas priklauso nuo plėtinio pasirinkimo. Jei ši hipotezė pasitvirtintų, tai reikštų, kad matematikos tradicija kurti hierachnę abstrakcijų piramidę patyrė fiasko ir matematiką reikia reformuoti remiantis holistinio mąstymo paradigma. Fizikoje tai reikštų, kad elementari dalelė yra suderintinio Visatos laukų superpozicijos rezultatas ir atvirkščiai, o mikro ir makro tenkina tam tikrą apibrėžiantį ryšį, kas yra ekvivalentiška simetrijos tarp mikro ir makro (tarp viendalelinių ir kolektyvinių laisvės laipsnių) postulavimui. Kyla klausimas ar toks simetrijos reikalavimas nėra pažinimo, kaip visumos projekcijos (endomorfizmo) į savo dalį (pvz. žmogaus smegenis, informacinį tinklą ar pan.) rezultatas, o tokio atvaizdavimo nevienareikšmiškumą sąlygoja tokio endomorfizmo branduolys. Išeitų, kad agnostikai buvo teisūs, ir Pasaulis su tam tikromis išlygomis yra iš principo nepažinus ir mes tokias pažinimo spragas užpildome ad hoc tikėjimais (tarp jų ir religiniu), dažnai vadinamais hipotezėmis ar “sąmokslo teorijomis”. Tik mes per trumpai gyvename, kad tai pastebėtume ir mus, kaip atominės bombos sprogimas, akina modernaus mokslo bei technologijų laimėjimai, akindami ir atitraukdami mūsų dėmesį nuo išvirkčiosios (pvz. ekologinės) problemų pusės…
Kita vertus, natūriniai skaičiai, kaip konstruktyvus genetinis objektas, pagimdytas iš 1 ir “+” oprecijos sąvokų nepalieka pasirinkimo laisvės, kuri atsiranda, kai abstrahuojame ar formalizuojame, kaip kokie poetai, o tos laisvės sukurtų vaiduoklių ar “virtualių dvasių” vėliau tenka atsisakyti empirinio verifikavimo praktine patirtimi keliu… Būtent tokio požiūrio laikos konstruktyviosios ir intuityviosios matematikos mokyklos atstovai, kuriuos nustelbė formalistai. Kaip šmaikščiai pastebėjo John’as von Neumann’as, aksiomatinis metodas turi tokius pat pranašumus, kaip vagystė prieš sąžiningą darbą…
Tai reikštų, kad visa galima abstrakti aksiomatinė matematika yra skaičių teorijos modeliai, pagimdyti baigtinių natūrinių skaičių savybių poaibių bazėje, o pirminių skaičių paieškos algoritmas Eratosfeno (Eratosthenes) rėčių yra filosofinio agnosticizmo analogas – kiekvienas naujai atrastas pirminis skaičius pateikia siurprizą, kurio negalima išvesti iš praeities patirčių (atvirumas)…
Atleiskite už tokį platų “lyrinį” nukrypimą į filosofines pažinimo problemas. Net mokslinei Lietuvos visuomenės daliai šios problemų pusės yra mažai žinomos.

Reply
VILIJA says:

Saturday August 13th, 2016 at 03:37 PM

NESU MATEMATIKĖ, BET MAN PASIDARĖ AIŠKU.TAIGI YRA ĮSTABIOJI MATEMATIKA IR MATEMATIKOS KULTŪRA.
Jei norima mokyti ir mokytis matematikos, dera keisti matematikos programas ir mokytojų rengimą.
Kalimas ir reprodukcija matematikoje yra ne tai.O juk Valstybinio egzamino siekis buvo – mokinio logikos ugdymas.Tik kur kaip tai vyskta nesuprantu.

Reply
Rimas N says:

Saturday August 20th, 2016 at 09:04 AM

Kalimas ir reprodukcija mokyklinėje matematikoje yra mokymo metodas, kurio istorija nusitęsia daug tūkstančių metų atgal į praeitį. Toks mokymo metodas atitinka vaikų ruošimą prekybinei ir administracinei veiklai. Yra ir kitų mokymo metodų. Kalimas ir reprodukcija buvo ir yra naudojami, nes atitinka tam tikros visuomenės grupės poreikius. Problema atsiranda tada, kai toks mokymo metodas valstybėje tampa vieninteliu. Net tarpukario Lietuvoje buvo siekiama balanso matematikos mokyme, greta kalimo buvo siekiama diegti samprotavimą.

Mane vis labiau stebina tarpukario Lietuvos matematikų bendruomenės aktyvumas, lyginant su tuo, ką turime dabar. Kad ir neigiamųjų skaičių pagrindimo klausimas buvo diskusijų dalimi. Pavyzdžiui, mano tekste trečiasis aiškinimas buvo naudojamas straipsnyje A. Taškūnas. Neigiamųjų skaičių veiksmai. Švietimo darbas, 7, (1926).
http://www.epaveldas.lt/vbspi/biRecord.do?biExemplarId=157611&biRecordId=26168

Reply

Matematika kaip kultūros reiškinys

Kodėl neigiamųjų skaičių sandauga yra teigiamas skaičius?

3 Responses to “Kodėl neigiamųjų skaičių sandauga yra teigiamas skaičius?”

Leave a Reply Cancel reply