Kas yra matematinis mąstymas?

Šiame įraše pristatau Davido Tallo teorinę konstrukciją, kuri pakankamai išsamiai aiškina matematinį mąstymą, jo vystymąsi ir individualaus pobūdžio sunkumus atsirandančius mokantis ar studijuojant matematikos. D. Tallo teorija gali padėti pertvarkant matematikos mokymo turinį ir programą, bei matematikos pasiekimų rezultatų vertinimą.

Matematinis mąstymas yra viena iš matematinio ugdymo kompetencijų mūsų vidurinio mokslo programoje. Kitos kompetencijos yra žinios ir supratimas, matematinis komunikavimas, matematikos taikymas, problemų sprendimo gebėjimai ir mokėjimas mokytis. Šios kompetencijos apibūdina matematinį kompetetingumą vidurinėje mokykloje. Dar sudėtingesnis klausimas būtų dėl tokios kompetetingumo sampratos adekvatumo, bet čia jo nesvarstome. Matematikos vidurinio ugdymo bendrojoje programoje teigiama, kad  ,,Matematinį mąstymą mokiniai parodo (4.7.1-4.7.6):

• keldami hipotezes probleminėse situacijose ir jas tikrindami;
• analizuodami problemą, uždavinį suskaido į lengviau įveikiamas, geriau išnagrinėtas dalis;
• nustatydami objektų bei reiškinių sąryšius ir dėsningumus;
• įrodydami teiginių teisingumą;
• darydami tikslias logines išvadas, jas pagrįsdami, argumentuodami, apibendrindami;
• demonstruodami matematinių idėjų originalumą.

Nepublikuotame straipsnyje (14 pusl.) rašiau, kad pirmos trys ir penktoji savybės yra gerai žinomi  mokslinės veiklos principai taikomi gamtos ir visuomenės tyrimams. Apie ketvirtąją savybę rašiau, kad jos neįmanoma realizuoti, nes moksleiviai nėra supažindinami su tiksliomis matematikos sąvokų apibrėžtimis ir logikos elementais.  Paskutinės, šeštosios savybės, iki šiol nesuprantu.

Vien kritikos nepakanka. Norint bent kiek konkrečiau kalbėti apie matematikos mokymo tikslus ir pasiektus rezultatus, reikia susitarti dėl tikslaus frazės ,,matematinis mąstymas“ interpretavimo. Tai nėra lengva, nes ši frazė naudojama neįprastai dažnai. Pavyzdžiui, Google paieškos sistema internete pateikia apie 640000 įrašų su fraze “mathematical thinking“. 2012 metais Sean Argyle apgynė mokslų daktaro disertaciją “Mathematical Thinking: From Cacophony to Consensus“, kurioje bandoma nustatyti bendrą požiūrį į matematinį mąstymą. Galima būtų apsiriboti kitų šalių mokyklinės matematikos programų (curriculum) peržiūra. Bet rezultatas yra panašus, kaip ir su Google paieška: didelė įvairovė ir maža tikslumo.

Matematikai matematiniu mąstymu vadina logiškai tikslų samprotavimą apie matematikos sąvokas. Nematematikui šis apibūdinimas mažai prasmingas. Norėdamas paaiškinti matematinį mąstymą nematematikui Keithas Devlinas siūlo  tokį palyginimą:

To people whose experience of mathematics does not extend far, if at all, beyond the high school math class, I think it’s actually close to impossible for them to really grasp what mathematical thinking is. I used to try to convey the distinction with an analogy. “K-12 mathematics is like a series of courses in digging trenches, pouring concrete, bricklaying, carpentry, plumbing, electrical wiring, roofing, and glazing,” I would say. And then, after a brief pause, I would continue,  “Mathematical thinking is the equivalent of architecting. You need all of those individual house-building skills to build a house. But putting those skills together and making use of them requires a higher-order form of thinking. You need someone who can design the building and oversee its construction.”

Siekdamas tiksliau paaiškinti matematinį mąstymą Keithas Devlinas parašė knygutę Introduction to Mathematical Thinking  ir organizavo atitinkamą  video kursą. Šis kursas tinkamas tiems, kuriems reikalinga pagalba pereinant nuo mokyklinės matematikos prie universitetinės matematikos, t.y. pirmo kurso universiteto studentams, nebūtinai matematikams. Toliau aptarsime matematinio mąstymo sampratą, kuri yra tam tikra prasme gilesnė ir bendresnė.

Davido Tallo trys matematinio mąstymo sudėtingumo formos.

D. Tallo teorija grindžiama neuromokslo siūloma bendrąja žmogaus mąstymo samprata, kuri savo ruožtu remiasi  neuronų jungčių susidarymo smegenyse teorija. Matematinio mąstymo sudėtingumo vystymąsi apsprendžia trijų matematinio žinojimo formų plėtra. Trumpai apibūdinsime matematinių žinių įgijimo būdus.

Stebint realius objektus, protu suvokiamos jų savybės ir išreiškiamos kalba. Laikui bėgant, savybių apibūdinimas tampa tikslesniu ir įgyja žodinės apibrėžties formą, panašią į tą, kuri naudojama Euklido geometrijoje. Tiems, kas studijuoja matematiką universitete, realių objektų savybių apibūdinimai įgija dar bendresnes aksiomines formas, tokias kaip neeuklidinė geometrija, diferencialinė geometrija ar topologija.

Kitaip įsisavinamos aritmetikos žinios. Šiuo atveju apibendrinami veiksmai su realiais objektais, bet ne jų savybės. Tokiais veiksmais su objektais gali būto skaičiavimas, grupavimas, tvarkymas, sudėjimas, atėmimas, dauginimas, dalijimas. Palaipsniui šie veiksmai tampa pagrįstomis matematinėmis operacijomis, kurios išreiškiamos simboliais. Savo ruožtu, simboliai pasidaryti suvokiami ne tik kaip operacija, bet kaip suglausta sąvoka . Pavyzdžiui, objektų skaičiavimo veiksmai išsivysto į aritmetines operacijas, o skaičiai tampa simboliais su kuriais atliekamos aritmetinės operacijos. Dar bendresne forma skaičių aritmetikos apibūdinimas tampa naudojant Peano aksiomas. Kita aritmetikos apibendrinimo forma yra algebra.

Aprašyti matematikos žinių įgijimo būdai sudaro tris skirtingas matematikos žinių formas:

1. sąvokos gaunamos stebint objektus ir apmąstant jų savybes (mintinis eksperimentas);
2. sąvokos gaunamos stebint operacijas su objektais ir apmąstant jų savybes;
3. aksiomų pagalba apibrėžiamos sąvokos ir įrodymų būdu gaunamos objektų savybės.

Pirmose dviejose  žinojimo formose sąvoka gaunama iš objektų stebint savybes ar operacijas, o trečioji forma, atvirkščiai, objektai ir jų savybės gaunami iš sąvokos. Pirma ir antra žinių formos gali papildyti viena kitą. Šias tris žinojimo formas D. Tallas vadina Three Worlds of Mathematics, o kiekvieną iš jų vadina, atitinkamai, World of Conceptual Embodiment, World of Symbolic Calculation ir World of Axiomatic Formalism:

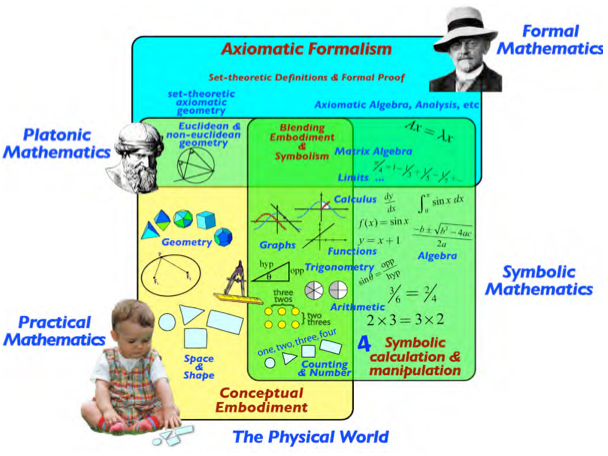
Šias tris matematikos žinių formas pirmą kartą apibūdino  Gray and Tall, 2001, taip pat žiūrėk D. Tall 2004. Paveikslas paimtas iš E.R. Ronda tinklaraščio.

Kaip šios trys žinių formos atsispindi, pavyzdžiui, realiojo skaičiaus sąvokoje? Realaus skaičiaus sąvoka yra visų trijų formų derinys: taškas skaičių tiesėje tai pirmoji forma, begalinė dešimtainė trupmena yra antroji forma ir pilnas sutvarkytas laukas yra trečioji forma.  Pavyzdžiui, skaičių tiesės geometrinė (abstrakti) samprata atsiranda mąstant apie pieštuku nubrėžtą tiesią linija ant popieriaus. Suvokiant skaičių tiesę, realusis skaičius apibrėžiamas kaip taškas ant tokios tiesės. Kiek man žinoma, Lietuvoje tik natūralieji skaičiai siejami su taškais ant skaičių tiesės, racionalūs skaičiai apibrėžiami įvairiausiais kitais būdais, o realieji skaičiai visai neapibrėžiami (daugiau apie tai yra mano pranešime). Kartais realieji skaičiai apibrėžiami kaip begalinės dešimtainės trupmenos, kurias galima priskirti antrajai žinių formai. Straipsnyje The Transition to Formal Thinking in Mathematics  D. Tallis rašo kaip jo teoriniame kontekste atrodo kitos matematinės analizės sąvokos. Netrukus turi pasirodyti D. Tallo knyga How Humans Learn to Think Mathematically, kurios pirmas skyrius yra čia.

Taigi, matematinis mąstymas pagal D. Tallą, yra matematikos žinių įgijimo būdas apibūdinamas viena iš trijų formų (Three Worlds of Mathematics) arba jų deriniu. Tokia matematinio mąstymo samprata atskleidžia tai, kaip formuojasi matematikos sąvokų ir matematikos objektų supratimas. Skirtingoms sąvokoms ir objektams tas supratimas formuojasi skirtingai ir į tai reikia atsižvelgti mokant matematikos ar ją studijuojant. Aiškinantis kai kurias sąvokas (pvz. natūraliuosius skaičius) naudinga pradėti nuo realaus pasaulio konteksto. Tačiau tolesniam skaičiaus sampratos aiškinimui reikalingi abstraktūs objektai (skaičių tiesė – pirma forma, dešimtainės trupmenos – antra forma, aksiominis skaičių laukas – trečia forma). Pirmos dvi matematikos žinių formos paprastai yra pradinio ir vidurinio matematinio ugdymo turiniu, o trečioji žinių forma – universitetinių studijų turiniu. Tiesa, Lietuvoje taip nėra, nes mes vis dar mokome tokią matematiką, kokia ji buvo iki 18 amžiaus.

Jano Sniadeckio matematinio mąstymo samprata

Kad įsitikinti paskutiniu teiginiu pacituosiu Jano Sniadeckio pranešimą ,,Apie matematinį mąstymą“, skaitytą Vilniaus imperatoriškojo universiteto mokslinėje sesijoje 1818 m. balandžio 15 d. Savo pranešimo pradžioje jis pabrėžia

,,…matematikos moksluose gali būti vadinama matematiniu mąstymu tik, tai, kas paaiškinama, išvedama ir įrodoma skaičiavimu.“

Mūsų mokyklinė matematika tokios sampratos nediegia. Antroje pranešimo dalyje, apibendrindamas Sniadeckis sako:

Pirma. Matematinis mąstymas grindžiamas mokėjimu skaityti ir vartoti kalbą, mokėjimu patikimai ir sąryšingai reikšti tiesas bei gerai apmąstytas idėjas, skaičiavimo nulemtos tvarkos, sąryšio ir kilmės matymu.

Antra. Sutalpindamas daugybę idėjų ir jas apimdamas tikslia simboline išraiška, skaičiavimas yra intelektualinių galių atrama ir atminties apsauga, o kartu ir didelė parama tas idėjas lyginant ir susiejant. Vertinga gėrybė, kurios neturi jokie kiti mokslai.

Trečia. Keliai, kuriuos šis skaičiavimas praeina, yra tikrumo vieškelis, kuriame negalima sutikti nieko abejotino nei klaidingo, kas galėtų intelektą nukreipti nuo tiesos kelio. Kita didelė vertybė, skirta vien tik matematikai!

Ketvirta. Skaičiuoti be nuolatinio atidumo ir protavimo – tai mokytis ne mokslo, bet jo mechanizmo.

Penkta. Atsidėjus ir supratingai sudarytas skaičiavimo mechanizmas teikia greitesnį dalyko matymą ir, dažnai jį atliekant, pasiūlo naujus ir lengvesnius kelius bei metodus.

Šešta. Skaičiavimo aiškinimui suteikti tai, ko jame neaptinkama, arba jį apsvarstyti pasitelkus metafiziką – tai klastoti mokslą ir intelektą nuvesti nuo tiesos bei tikrumo kelio.

Septinta. Visi skaičiavimo paradoksai ir keistenybės atsiranda iš to, kad arba jį blogai skaitome, arba dar nežinome kažkokios tiesos, dėl kurios nežinojimo jie būtinai kyla.

Iš viso to nesunku suprasti paslaugos, kurią skaičiavimas teikia vadinamiesiems faktais, stebėjimais ir eksperimentais grindžiamiems mokslams, nepajėgiant šiuose moksluose protavimo susieti į vieną nagingą nuolatinio ir nepajudinamo tikrumo grandinę, svarbą: juk kai šie mokslai neparemti skaičiavimu, jie nesiliauja buvę arba paprastos erducijos rinkiniu, arba, taip sakant, nuolat kintančių teorijų ir nuomonių klampyne.

Cituota iš Janas Sniadeckis. Raštai. Filosofijos darbai. Iš lenkų kalbos vertė Romanas Plečkaitis. Margi Raštai, Vilnius, 2007.