Mokyklinės matematikos turinys: išvestinė (tęsinys)

Mokyklinė matematika Add comments

Grd 282015

Šį ir ankstesnius įrašus apie mokyklinės matematikos turinį skiriu matematikos mokytojui. Juose skirtingais aspektais kalbama apie tradicines elementariosios matematikos sąvokas neatsisakant samprotavimų loginio tikslumo. Šiame įraše pagrindinį dėmesį skiriu J. Marsdeno ir A. Weinsteino pasiūlytai išvestinės sampratai iš knygos Calculus Unlimited (1981). Jų išvestinė ypatinga tuo, kad apibrėžime naudojamos paprasčiausios funkcijų savybės ir nėra naudojama $\epsilon-\delta$ ribos samprata. Nepaisant to, Marsdeno-Weinsteino išvestinė ekvivalenti tradicinei išvestinei, kuri yra skirtuminio santykio riba išreiškiama $\epsilon-\delta$ terminais. Anksčiau apie kitas išvestinės formas rašiau čia ir čia.

Motyvacija Marsdeno-Weinsteino išvestinės apibrėžimui. Tarkime, kad objektas juda išilgai tiesės kuria nors kryptimi. Jo judėjimą galima apibūdinti funkcija f išreiškiančia priklausomybę tarp nueito kelio y ir judėjimo laiko x, t.y. y = f(x). Paprasčiausią judėjimą apibūdina afininė funkcija. Būtent, tegul d ir m yra realieji skaičiai. Funkcija L su reikšmėmis L(x) = d + m x kiekvienam x iš R vadinama afinine. Mokyklinėje matematikoje funkcija L vadinama tiesine, nes jos grafikas tiesė. Analizinėje geometrijoje L(x) vadinama tiesės L lygtimi, o m vadinamas šios tiesės krypties koeficientu

Sakoma, kad objekto judėjimas yra tolygus, jei jo padėties priklausomybę nuo laiko išreiškianti funkcija yra afininė. Tolygaus judėjimo greičiu vadinamas jį išreiškainčios afininės funkcijos krypties koeficientas. Šis greitis nepriklauso nuo laiko arba, kitaip tariant, yra pastovus. Mus domina klausimas: kaip apibūdinti netolygaus judėjimo greitį?

Atsakant į šį klausimą reikia sugalvotį taisyklę, kuri kiekvienam laiko momentui priskirtų judėjimo kintamumą apibūdinantį skaičių. Tokia taisyklė vadinama momentiniu greičiu. Netolygiai judančio objekto momentinio greičio taisyklę fiksuotu laiko momentu galima bandyti įvertinti netolygų judėjimą lyginant su tolygiu judėjimu.

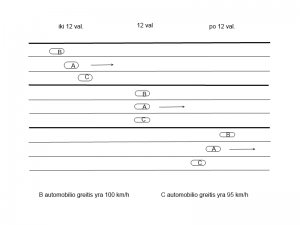
Tarkime, kad automobilis A juda netolygiai trijų juostų kelyje vidurine juosta. Vertinsime A automobilio momentinį greitį 12 valandą. Jo judėjimą lyginsime su pirmąja ir trečiąja juostomis tolygiai judančiais automobiliais B ir C. B automobilio greitis 100 km/h ir C automobilio greitis 95 km/h. Tarsime, kad 12 valandą visi trys automobiliai susilygino kelyje. Iki 12 valandos ir po 12 valandos automobilių padėtį vaizduoja piešinys:

Šio vertinimo rezultatu yra faktas, kad A automobilio momentinis greitis 12 valandą buvo tarp 95 km/h ir 100 km/h. Tikslinant vertinimą reikėtų keisti tolygiai judančių B ir C automobilių greičius.

Apibendrinant šį vertinimą tarkime, kad netolygiai judančio automobilio A nueito kelio priklausomybę nuo laiko išreiškia funkcija f, o tolygiai judančius automobilius B ir C apibūdina afininės funkcijos L₁ ir L₂, atitinkamai. Iki 12 valandos A ir B automobilių nueito kelio skirtumas išreiškiamas funkcijų skirtumo f – L₁ reikšme buvo neigiamas, A ir C automobilių nueito kelio skirtumas f – L₂ buvo teigiamas. Po 12 valandos šių skirtumų ženklai pasikeitė. Toks vertinimas gali būti tęsiamas mažinant tolygiai judančių automobilių greičių skirtumą. Jei pavyksta šį skirtumą sumažinti iki vieno skaičiaus, tai jis ir galėtų būti netolygiai judančio automobilio momentinis greitis.

Marsdenas ir Weinsteinas panaudojo šį momentinio greičio vertinimo būdą apibrėždami savo funkcijos išvestinės variantą.

Marsdeno-Weinsteino išvestinė. Pagrindine funkcijos savybe naudojama apibrėžiant išvestinę yra jos ženklo pasikeitimas kertant $x$ -ų ašį.

Apibrėžtis. Tegul $g$ yra funkcija iš R į R ir $c$ yra realusis skaičius. Sakoma, kad taške $c$ funkcija $g$ keičia ženklą iš neigiamo į teigiamą, jei egzistuoja toks atvirasis intervalas $(a,b),$ kuriam priklauso $c$ ir teisingi du teiginiai (implikacijos):

(1) jei $a<x<c,$ tai $g(x) < 0$ ir (2) jei $c<x<b,$ tai $g(x) > 0.$

Atvirkščiai, sakoma, kad taške $c$ funkcija $g$ keičia ženklą iš teigiamo į neigiamą, jei egzistuoja toks atvirasis intervalas $(a,b),$ kuriam priklauso $c$ ir teisingi du teiginiai (implikacijos):

(1) jei $a<x<c,$ tai $g(x) > 0$ ir (2) jei $c<x<b,$ tai $g(x) < 0.$

Tegul $f$ yra funkcija ir $c$ yra realusis skaičius priklausantis $f$ apibrėžimo sričiai. Jei $L$ yra afininė funkcija su reikšmėmis $L(x) = d + m x$ kiekvienam $x$ iš R, tai jos grafikas eina per tašką $(c,f(c))$ kai $d=f(c)-mc$ . Sakysime, kad funkcija $L_u$ su reikšmėmis $L_u(x) = f(c) + u(x-c)$ yra afininė funkcija per tašką $(c,f(c)).$

Apibrėžtis. Tegul $f$ yra funkcija iš R į R, $c$ yra realusis skaičius ir $L_u$ _, $u\in{\bf R}$ , yra rinkinys afininių funkcijų per tašką $(c,f(c)).$ Sakysime, kad funkcija $f$ diferencijuojama Marsdeno-Weinsteino prasme taške $c,$ jei egzistuoja toks realusis skaičius $m$ , kuriam teisingi du teiginiai:

(1) kiekvienam $u > m$ taške $c$ funkcija $f-L_u$ keičia ženklą iš teigiamo į neigiamą ir

(2) kiekvienam $u < m$ taške $c$ funkcija $f-L_u$ keičia ženklą iš neigiamo į teigiamą.

Skaičių $m,$ apibrėžtą šiais dviem teiginiais, vadinsime funkcijos $f$ MW-išvestine taške $c$ ir žymėsime $f_{MW}'(c) := m.$

MW-išvestinė, jei egzistuoja, yra vienintelė. Iš tikro, jei yra du skirtingi skaičiai $m_1$ ir $m_2$ tenkinantys MW-išvestinės apibrėžimą, tai skaičius $m$ lygus $(m_1+m_2)/2$ yra tarp $m_1$ ir $m_2$ . Tokiu atveju funkcija $f-L_m$ taške $c$ turėtų keisti ženklą iš teigiamo į neigiamą ir iš neigiamo į teigiamą, kas yra neįmanoma.

Paprasčiausi MW-išvestinės skaičiavimo pavyzdžiai. Marsdeno ir Weinsteino knygoje Calculus Unlimited yra daug MW-išvestinės skaičiavimo pavyzdžių. Taip pat ir jos taikymo pavyzdžių tiriant funkcijas. Čia apsiriboju paprasčiausiu pavyzdžiu norėdamas tik iliustruoti sąvokos naudojimą.

Tarkime, kad $f$ yra funkcija su reikšmėmis $f(x)=x^2$ visiems $x\in {\bf R}$ ir $c$ yra realusis skaičius. Rasime šios funkcijos MW-išvestinę taške $c$ . Šiuo atveju funkcija $f-L_u$ įgyja reikšmes

$f(x)-L_u(x)=x^2-[c^2+u(x-c)]=(x-c)(x+c-u).$

Ši funkcija taške $c$ keičia ženklą iš neigiamo į teigiamą kai $c>u-c$ arba kai $u < 2c.$ Kadangi ši savybė turi būti teisinga kiekvienam $u < m,$ tai turi būti teisinga nelygybė $m\leq 2c.$ Atvirkščiai, ši funkcija taške $c$ keičia ženklą iš teigiamo į neigiamą kai $c<u-c$ arba kai $u > 2c.$ Kadangi ši savybė turi būti teisinga kiekvienam $u > m,$ tai turi būti teisinga nelygybė $m\geq 2c.$ Taigi, reikšmė $m = 2c$ yra funkcijos $f(x)=x^2$ MW-išvestinė taške $c.$

Sudėtingesniems pavyzdžiams, tokiems kaip $f(x)=f(c)+(x-c)p(x),$ verta prieš tai įsisavinti tolydumo sąvoką.

MW-išvestinė ir Weierstrasso išvestinė. Geriausiai naują sąvoką paaiškina jos palyginimas su jau žinoma sąvoka. Įprasta išvestinė yra apibrėžiama kaip riba Weierstrasso prasme, arba, kaip dar sakoma, riba $\epsilon-\delta$ terminais. Priminsiu šią sąvoką.

Apibrėžtis. Tegul $f$ yra funkcija iš R į R ir $c$ yra realusis skaičius. Sakoma, kad $f$ diferencijuojama (Weierstrass‘o prasme) taške $c,$ jei egzistuoja toks realusis skaičius $m,$ kuriam teisingas teiginys: kiekvienam $\epsilon > 0$ egzistuoja toks $\delta > 0$ , kad bet kuriam $x\in {\bf R}$ teisinga implikacija

jei $0 < |x-c| < \delta,$ tai $|\frac{f(x)-f(c)}{x-c}-m|<\epsilon.$

Kitaip tariant, jei egzistuoja riba $\lim_{x\to c}\frac{f(x)-f(c)}{x-c}.$ Jei $f$ diferencijuojama taške $c,$ tai riba (skaičius $m$ ) vadinama funkcijos $f$ išvestine taške $c$ ir žymima $f'(c).$

Teorema. Tegul $f$ yra funkcija iš R į R ir $c$ yra realusis skaičius. Skaičių $m$ apibūdinantys teiginiai (i) ir (ii) yra ekvivalentūs, čia

(i) egzistuoja MW-išvestinė $f_{MW}'(c)$ ir lygi $m;$

(ii) egzistuoja išvestinė $f'(c)$ ir lygi $m.$

Įrodymas. Pirma, įrodysime implikaciją iš (i) į (ii). Tarkime, kad egzistuoja MW-išvestinė $f_{MW}'(c)$ ir lygi $m.$ Tegul $\epsilon>0$ ir $u=m+\epsilon.$ Pagal prielaidos pirmąją dalį, egzistuoja taško $c$ aplinka $(a,b),$ kurioje funkcija $f-L_u$ keičia ženklą iš teigiamo į neigiamą. Tegul $\delta_1=\min\{c-a,b-c\}.$ Kai $x\in (c-\delta_1,c),$ tai

$f(x)-[f(c)+u(x-c)]>0$ arba $f(x)-f(c)>(m+\epsilon)(x-c).$

Kadangi $x-c<0,$ tai, padalinę pastarąją nelygybę iš $x-c$ ir pertvarką, gauname

$\frac{f(x)-f(c)}{x-c}-m<\epsilon.\qquad\qquad (1)$

Kai $x\in (c,c+\delta_1),$ tai

$f(x)-[f(c)+u(x-c)]<0$ arba $f(x)-f(c)<(m+\epsilon)(x-c).$

Padalinę pastarąją nelygybę iš $x-c$ ir pertvarką, gauname tą pačią (1) nelygybę. Taigi, (1) nelygybė teisinga tiems $x$ , kuriems $0<c-x<\delta_1.$

Tegul $u=m-\epsilon.$ Panašiai naudodami prielaidos antrąją dalį, gauname tokį $\delta_2>0,$ kad nelygybė

$\frac{f(x)-f(c)}{x-c}-m>-\epsilon.\qquad\qquad (2)$

teisinga tiems $x,$ kuriems $0<|x-c|<\delta_2.$ Tegul $\delta=\min\{\delta_1,\delta_2\}>0.$ Tada, apjungę (1) ir (2) nelygybes, gauname, kad nelygybė

$|\frac{f(x)-f(c)}{x-c}-m|<\epsilon$

teisinga tiems $x,$ kuriems $0<|x-c|<\delta.$ Teiginys (ii) įrodytas.

Antra, įrodysime implikaciją iš (ii) į (i). Tarkime, kad egzistuoja išvestinė $f'(c)$ ir lygi $m.$ Pasirinktam $u\not =m$ įvertinsime funkcijų skirtumo $f-L_u$ ženklą taško $c$ aplinkoje. Tegul $u>m$ ir $\epsilon =u-m.$ Pagal prielaidą egzistuoja toks $\delta >0,$ kad nelygybė

$\frac{f(x)-f(c)}{x-c}<m+\epsilon=u\qquad\qquad (3)$

teisinga visiems $x,$ kuriems $0<|x-c|<\delta.$ Tegul $x\in (c-\delta,c).$ Tada $x-c<0$ ir, daugindami (3) nelygybę iš $x-c,$ gauname

$f(x)-f(c)>u(x-c)$ arba $f(x)-L_u(x)>0.$

Tegul $x\in (c,c+\delta).$ Tada $x-c>0$ ir, daugindami (3) nelygybę iš $x-c,$ gauname

$f(x)-f(c)<u(x-c)$ arba $f(x)-L_u(x)<0.$

Gavome, kad taško $c$ aplinkoje $(x-\delta,c+\delta)$ funkcija $f-L_u$ keičia ženklą iš neigiamo į teigiamą, t.y. galioja MW išvestinės pirmoji dalis. Kai $u<m,$ imdami $\epsilon =m-u$ ir panašiai samprotaudami gauname, kad taško $c$ aplinkoje funkcija $f-L_u$ keičia ženklą iš teigiamo į neigiamą, t.y. galioja MW išvestinės antroji dalis. Teiginys (i) ir, tuo pačiu, teorema yra įrodyti.

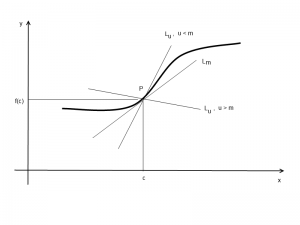
MW-išvestinė ir funkcijos grafiko liestinė. Prieš metus įkėliau įrašą, kuriame priminiau apie Irl C. Bivenso pasiūlytą funkcijos grafiko liestinės apibūdinimą. Įraše parodyta, kad funkcijos grafikas turi liestinę taške tada ir tik tada, kai egzistuoja išvestinė tame taške. Šis faktas kartu su pastarąja teorema įrodo, kad funkcijos grafiko liestinės egzistavimas taške taip pat ekvivalentus MW-išvestinės tame taške egzistavimui. Norint geriau suprasti išvestinę galima bandyti tiesiogiai palyginti liestinės egzistavimą su Marsdeno-Weinsteino išvestine. Priminsiu liestinės sąvoką.

Apibrėžtis. Tegul $f$ yra funkcija iš R į R ir $c$ yra realusis skaičius. Tiesė $L$ nubrėžta per tašką $P=(c,f(c))$ vadinama funkcijos $f$ grafiko liestine taške $P$ , jei su kiekviena kita tiese $K$ einančia per tašką $P$ egzistuoja tokia taško $c$ aplinka $(a,b),$ kad nelygybė

$|f(x)-L(x)|\leq |f(x)-K(x)|$

teisinga kiekvienam $x\in (a,b).$

Kaip jau minėta, jau įrodytų faktų išvada yra teiginys

Išvada. Tegul $f$ yra funkcija iš R į R ir $c$ yra realusis skaičius. Skaičių $m$ apibūdinantys teiginiai (i) ir (ii) yra ekvivalentūs, čia

(i) egzistuoja MW-išvestinė $f_{MW}'(c)$ ir lygi $m$ ;

(ii) kiekvienam skaičiui $u$ egzistuoja tokia taško $c$ aplinka $(a,b),$ kad nelygybė

$|f(x)-L_m(x)|\leq |f(x)-L_u(x)|\qquad\qquad (4)$

teisinga kiekvienam $x\in (a,b).$

Kitos lemos įrodymas rodo, kad galima tiesiogiai įrodyti pastarosios išvados implikaciją iš (ii) į (i).

Lema. Tegul $f$ yra funkcija iš R į R, $c, m, u$ yra realieji skaičiai ir $u>m.$ Tarkime, kad visiems $x$ iš taško $c$ aplinkos $(a,b)$ teisinga (4) nelygybė. Tada funkcijų skirtumas $f-L_u$ taško $c$ aplinkoje $(a,b)$ keičia ženklą iš teigiamo į neigiamą.

Įrodymas. Kiekvienam skaičiui $x$ teisinga tapatybė

$f(x)-L_u(x)=f(x)-L_m(x)+(m-u)(x-c).\qquad\qquad (5)$

Parodysime, kad (4) nelygybė, pastaroji tapatybė ir jos paskutiniojo nario ženklas apsprendžia skirtumo $f(x)-L_u(x)$ ženklą. Tegul $x\in (a,c).$ Tokiems $x$ ir $u>m$ teisinga nelygybė

$(m-u)(x-c) > 0.\qquad\qquad (6)$

Norėdami įrodyti, kad $f(x)-L_u(x)>0$ tarkime, kad teisinga priešinga nelygybė $f(x)-L_u(x)\leq 0.$ Naudodami (6) nelygybę ir (5) tapatybę, gauname $f(x)-L_m(x)<0.$ Panaudojus šiuos reikšmių ženklus vertinant modulius, (4) nelygybė įgyja išraišką

$-[f(x)-L_m(x)]\leq -[f(x)-L_u(x)].$

Suprastinę, gauname nelygybę $(m-u)(x-c)\leq 0,$ kuri prieštarauja (6) nelygybei. Todėl nelygybė $f(x)-L_u(x)>0$ teisinga atveju $x\in (a,c).$

Tegul $x\in (c,b).$ Lyginant su (6), tokiems $x$ ir $u>m$ teisinga kita nelygybė

$(m-u)(x-c) < 0.\qquad\qquad (7)$

Norėdami įrodyti, kad $f(x)-L_u(x)<0$ tarkime, kad teisinga priešinga nelygybė $f(x)-L_u(x)\geq 0.$ Naudodami (7) nelygybę ir (5) tapatybę, gauname $f(x)-L_m(x)>0.$ Panaudojus šiuos reikšmių ženklus vertinant modulius, (4) nelygybė įgyja išraišką

$f(x)-L_m(x)\leq f(x)-L_u(x).$

Suprastinę, gauname nelygybę $(m-u)(x-c)\geq 0,$ kuri prieštarauja (7) nelygybei. Todėl nelygybė $f(x)-L_u(x)<0$ teisinga atveju $x\in (c,b).$ Lema įrodyta.

Analogiška lema įrodoma atveju $u<m.$ Abi šios lemos įrodo išvados implikaciją iš (ii) į (i) tiesiogiai. Kol kas man nepavyko tiesiogiai įrodyti atvirkštinės implikacijos.

Kokia MW-išvestinės prasmė? Kadangi tai ne pirmas ir gal būt ne paskutinis mano įrašas skirtas išvestinės sąvokai, galima klausti kokia prasmė yra nagrinėti dar ir dar vieną ekvivalenčią sąvoką. J. Marsdenas ir A. Weinsteinas savo išvestinės sampratos vertę mato tame, kad jos apibrėžime tiesiogiai nenaudojama riba K. Weierstrasso prasme. Paplitusi nuomonė, kad pirmą kartą susipažįstančiam su analize žmogui, tris loginius kvantorius apimantis teiginys gali kelti sunkumų. MW-išvestinėje tokia teiginio forma yra užslėpta. Savo knygoje Calculus Unlimited autoriai parodo savo išvestinės sampratos galią įrodydami pagrindinius analizės faktus.

Mano nuomone, sąvokos naudingumas priklauso nuo įvairiausių aplinkybių ir poreikių. Aš vertinu MW-išvestinę kaip dar vieną funkcijos tyrimo priemonę ir aspektą. Kuo tokių priemonių daugiau, tuo geriau suprantamas matematinis objektas. Matematikos istorija rodo, kad išvestinės idėja rutuliavosi ilgai, kas patvirtina objekto ir sąvokos fundamentalumą. Kaip dažnai matematikoje tokiais atvejais atsitinka, bendras sutarimas dėl sąvokos apibrėžimo ateina po ilgo evoliucijos laikotarpio. J. V. Grabiner savo istorinėje apžvalgoje rašo:

Historically speaking, there were four steps in the development of today’s concept of the derivative, which I list here in chronological order. The derivative was first used; it was then discovered; it was then explored and developed; and it was finally defined. That is, examples of what we now recognize as derivatives first were used on an ad hoc basis in solving particular problems; then the general concept lying behind these uses was identified (as part of the invention of the calculus); then many properties of the derivative were explained and developed in applications both to mathematics and to physics; and finally, a rigorous definition was given and the concept of derivative was embedded in a rigorous theory.

Tiesą sakant, vargu ar yra pasiektas tas bendras sutarimas dėl išvestinės sąvokos. Jos samprata priklauso nuo ne mažiau fundamentalių tolydumo ir diskretumo, baigtinumo ir begalinumo sąvokų. Dėl jų ginčai neblėsta.

One Response to “Mokyklinės matematikos turinys: išvestinė (tęsinys)”

Pliadisfoto says:

2018.05.11 at 09:25

Kaip idomu!

Atsakyti

Matematika kaip kultūros reiškinys

Mokyklinės matematikos turinys: išvestinė (tęsinys)

One Response to “Mokyklinės matematikos turinys: išvestinė (tęsinys)”

Leave a Reply Cancel reply