Jėzuitai ir matematika

Šis įrašas apie tai, kaip požiūris į matematiką 17 amžiuje paveikė Europos kultūrinį ir politinį vystymąsi.  Amiro Alexanderio knyga Infinitesimal: How A Dangerous Mathematical Theory Shaped The Modern World. Scientific American, 2014 atskleidžia autoriaus versiją. Šią knygą pristatau todėl, kad ji neįprastai gerai parašyta tokio pobūdžio klausimams svarstyti.  Jos supratimui gilus matematinis išsilavinimas nėra būtinas. Tai svarbu, nes absoliuti mūsų visuomenės dauguma nenori arba negali skaityti tekstų apie matematiką, kurią suvokia  taip, kaip buvo ir yra mokomi mūsų mokyklose.  

Alexanderio knygoje nagrinėjamos dvi istorijos. Kol kas aptariu vieną iš jų – kovą dėl begalinės mažybės idėjos tarp jėzuitų iš vienos pusės ir G. Galilei, B. Cavalieri, E. Torricelli ir kitų matematikų iš kitos pusės. Šios istorijos eiga galėjo turėti savų pasekmių ir mūsų kraštui per jėzuitų įkurtus Vilniaus kolegiją ir Vilniaus universitetą (Academia Universitas Societatis Iesu). 

Pavojingoji matematinė idėja

Alexanderio knyga – istorinė, nors dėstymo forma primena romano siužetą. Pagrindinis Alexanderio knygos tikslas  – parodyti, kaip viena matematikos idėja įtakojo politinį ir kultūrinį Europos šalių vystymąsi 17 amžiuje.  Ši matematikos idėja yra viena iš tolydumo sąvokos sampratos formų, kuri apibūdina tipiško tolydaus matematinio objekto struktūrą. Tolydaus matematinio objekto pavyzdžiais yra geometrinė tiesė, paviršius, laiko intervalas.  Tiesės struktūrą apibūdinantį konkretų teiginį toliau vadinu (matematine) prielaida.

Prielaida.  Tiesę sudaro taškų arba ,,nedalomųjų“ virtinė (angl. every line is composed of a string of points, or „indivisibles“,…). [cituoju iš A.Alexander. Infinitesimal; 9 pusl.]

Nedalomasis šioje prielaidoje yra viena iš daugelio begalinės mažybės sąvokos formų. Daugiau apie be galo mažus dydžius rašiau čia. Suformuluota prielaida kelia papildomus klausimus. Jei tiesę sudaro taškai, tai kokio dydžio ir kiek jų yra? Jei matematinis (abstraktus) objektas yra teigiamo dydžio, tai jis iš esmės dalus. Jei teigiamo dydžio taškų yra be galo daug, tai bet kuri tiesės dalis turėtų būti begalinio dydžio. Jei tiesė sudaro be galo daug nulinio dydžio taškų, tai pati tiesė taip pat turėtų būti nulinio dydžio. Tai abejonės, kurių paaiškinimo ir pagrindimo buvo ieškoma ne tik 17-ame amžiuje. Svarus to meto argumentas už prielaidos teisingumą buvo jos efektyvumas ieškant atsakymų į nežinomus klausimus apie įvairiausius matematinius objektus. Kaip ir Archimedesas antikos laikais, naujųjų laikų matematikai Kepleris, Cavalieri, Torricelli, Galileo naudojo šią prielaidą nustatant figūrų plotus ir tūrius.

Panašūs klausimai ir samprotavimai šių dienų matematikos požiūriu nekyla ir gali atrodyti naivūs. Šiuolaikinėje matematikoje priimta, kad geometrinė tiesė yra ,,tapatinama“ su realiųjų skaičių aibe. Šis tapatinimas yra Dedekindo-Cantoro aksioma teigianti, jog tarp tiesės ir realiųjų skaičių aibės egzistuoja abipus vienareikšmė ir tvarką išsauganti atitiktis. Šia prasme tiesė yra sudaryta iš be galo daug realiųjų skaičių aibės elementų. Taško dydis (Lebesgue) mato prasme yra nulis. Bet toks požiūris gali nekelti abejonių dėl mūsų įpročio ,,suprasti“ tai, kas visuotinai priimta ir nekvestionuojama.  Be to, šiuolaikiniam požiūriui sąlygos susidarė tik 19 amžiaus pabaigoje. Tiesės struktūros problema, taip pat vadinama kontinuumo problema, 17 amžiuje turėjo atrodyti gerokai kitaip. 

 Prielaida, kad tiesę sudaro nedalomųjų virtinė buvo vienareikšmiškai nepriimtina senovės graikų matematikoje. Ši prielaida prieštaravo logiškai nepriekaištingai pitagoriečių įrodytam faktui, kad egzistuoja nebendramatės tiesės atkarpos (angl. incommensurable line segments). Dvi atkarpos yra bendramatės, jei jų ilgių santykis išreiškiamas trupmena. Atrodė jei prielaida teisinga, tai bet kurios dvi atkarpos turėtų būti bendramatės, nes sudarytos iš tų pačių matematinių atomų. Prielaidos apie tiesės atominę struktūra teisingumas taip pat griauna Zeno iš Alėjos samprotavimų logiką (žr. čia). Tai paaiškina, kodėl,  būdama logiškai nepriekaištingo samprotavimo pavyzdžiu, geometrija dominavo senovės graikų matematikoje. Praėjus pusantro tūkstančio metų, 17 -ame mūsų eros amžiuje, matematikai vėl ima naudoti iki tol logiškai nepagrindžiamos prielaidos apie tiesos struktūrą. Naujai formuluojamas senasis metodas nėra vienareikšmiškai atmetamas. Bet susilaukia pasipriešinimo iš netikėtos pusės – jėzuitų, Hobbeso ir jo šalininkų, prancūzų karališkosios aukštuomenės ir anglikonų bažnyčios. Tai labai vaizdingai nušviečiama naujojoje  Alexanderio knygoje.

Švietimo vaidmuo jėzuitų veikloje

Pirmoji Alexanderio knygos dalis skirta Jėzaus Draugijai ir jos kovai su be galo mažais dydžiais. Kodėl abstrakti matematikos idėja tapo aistringos ir nuožmios politinės kovos dėmesio centre? Taip atsitiko todėl, kad Jėzaus Draugija, siekdama pagrįsti Popiežiaus valdžią, norėjo parodyti ją esant tvarkos ir hierarchijos valstybės valdyme įsikūnijimu.  Eukleideso geometrija su savo aksiominiu-dedukciniu įrodymo metodu atrodė kaip tvarkinga iš viršaus į apačią nukreipta struktūra ir todėl labai tiko jėzuitų tikslui. Tuo tarpu be galo mažų dydžių idėja atspindėjo jutimine patirtimi besiremiantį samprotavimą, kuriame loginis griežtumas aukojamas naudingumui. Tokiu būdu be galo mažų dydžių idėja buvo jėzuitų tapatinama su chaosu, netvarka ir iš apačios į viršų nukreiptos struktūros pavyzdžiu. Pastaroji struktūra jėzuitų buvo siejama su protestantizmu. 

Vadovaujama Ignatius of Loyola [Ignaco Lojolos] Jėzaus draugija susikūrė tada, kai Romos Katalikų Bažnyčia atrodė pralaiminti  Reformacijai.  1540 metais Popiežius Paulius III leido įkurti religinę draugiją, save vadinančią Jėzaus Draugija, kuri tarnautų Popiežiui ir Bažnyčiai kovoje prieš Reformaciją. Pagal pradinį sumanimą šios draugijos nariai pagal poreikį turėjo vykti į bet kurią pasaulio dalį kaip keliaujantys kunigai ir ginti Bažnyčios interesus. Netrukus jėzuitai suprato, jog dar stipresnė priemonė siekiant savo tikslų yra kokybiškas ir gilus švietimas. Naujų kolegijų ir universitetų steigimas visur, kur įmanoma  tapo svarbiausia jėzuitų misija. Kokybiškam švietimui buvo reikalingi aukšto lygio mokytojai ir rimta mokymo programa. Pirmąjį uždavinį sprendė 1551 metais Romoje įkurta Collegio Romano (Romos kolegija), kurioje dirbo ir mokėsi pagrindinės intelektualinės jėzuitų pajėgos. Tuo pačiu buvo rengiama mokymo programa, kurios galutinė forma Ratio studiorum patvirtinta 1599 metais. Jėzuitų draugija turėjo nepriekaištingą hierarchinę struktūra, kurios pagalba visa veikla kiekvienoje šalyje buvo valdoma ir kontroliuojama iš centro Romoje. 1556 metais Ignatius of Loyola mirties metais jau veikė 33 jėzuitų kolegijos, 1579 metais veikė 144 jėzuitų kolegijos, 1626 metais jau veikė 444 jėzuitų kolegijos bei 100 seminarijų ir mokyklų, 1749 metais veikė net 669 kolegijos bei 176 seminarijos ir mokyklos. Dauguma mokymo įstaigų buvo Europoje, bet ne visos. Kai kurios iš jų, į  rytus nuo Europos, pasiekė net Nagasaki, Japonija, o vakarų pusėje pasiekė Lima, Peru. Jėzuitų švietimo sistema tapo pirmąja ir tikriausiai vienintele tokio pobūdžio vieninga pasauline švietimo sistema.

Švietimas jėzuitams buvo priemonė įveikti Reformacijos plėtrą. Tai reiškė, kad švietimas nesiribojo religiniu mokymu. Gilus religinis mokymas buvo grindžiamas plačiomis filosofijos, gramatikos ir įvairių kalbų studijomis. Gilus išsilavinimas buvo priemonė suvilioti šalies vietinį elitą savo vaikus mokyti jėzuitų mokyklose. Vienas iš jėzuitų 1567 metais teigė [A.A. 53 pusl.]: „For us lessons and scholarly exercises are a sort of hook with which we fish for souls„.  Tokiu ,,kabliuku“ buvo hierarchiškai tvarkinga žinių sistema. Iš pradžių mokoma gramatikos ir kalbų, po to Aristotelio filosofija ir viską vainikuoja ,,mokslų karalienė“ – teologija. Šioje žinių sistemoje nebuvo nei vieno fakto ar tiesos, kurie prieštarautų katalikų teologijai. Hierarchinė žinių sistema buvo ne tik pedagoginė priemonė. Ji turėjo atspindėti autoritarinę visuomeninę tvarką ir griežtą hierarchiją. Reformacija jų požiūriu, kūrė netvarką, chaosą ir maišatį žmonių galvose. Šis skirtumas buvo siejamas ir su protestantišku universitetiniu išsilavinimu, kuriam buvo priskiriama ta pati netvarka žinių sistemoje. Jėzuitai tikėjo, kad švietimo sistemos tikslas ne laisvas keitimasis idėjomis, bet tam tikrų tiesų diegimas. Daugeliu atvejų jėzuitai savo tikslą pasiekė.

Jėzuitas Christopheris Clavius

Kokia matematikos vieta jėzuitų žinių sistemoje? Pirmus kelis dešimtmečius sekusius po Jėzaus Draugijos įsteigimo 1540 metais matematikos buvo mokoma tiek, kiek jos reikėjo kitoms aukštesnio lygmens disciplinoms. Tačiau vienas žmogus savo gyvenimo tikslu padarė tokios padėties pakeitimą. Jo pastangų dėka matematika atsidūrė jėzuitų mokymo programos centre. Jėzuitai tapo ne tik kvalifikuotais matematikos mokytojais, bet tarp jų atsirado ir visoje Europoje žinomų matematikų. Tas žmogus buvo vokiečių matematikas ir astronomas jėzuitas  Christopher Clavius (1538-1612)  [Christophoras Clavijus, Kristoforas Klavijus].

Christopheris Clavius buvo talentingas matematikos mokytojas, puikių matematikos vadovėlių rašytojas ir aistringas  matematikos populiarintojas. 1574 metais išleido Eukleideso Pagrindų variantą įterpdamas ir savo mintis. Dėl šio veikalo Clavius vadinamas 16 amžiaus Eukleidesu. Christopherio Claviuso matematinis palikimas surinktas jo raštuose. Bet geriausiai žinomas savo prisidėjimu keičiant Julijaus kalendorių į Grigaliaus kalendorių. Šis Romos Katalikų Bažnyčios darbas labai pasitarnavo jos autoriteto grąžinimui. Šią sėkmę buvo siekiama pakartoti naudojantis matematikos autoritetu. A. Alexanderis rašo [63 pusl.]:

 If only the secret of the calendarical triumph could be infused into those other fields, the ultimate victory of Pope and Church would be assured. Clavius believed that he knew what this secret was: mathematics. Theological and philosophical disputes could rage forever, he believed, because there was no universally accepted way to decide who was right and who was wrong. Even when one side possessed the absolute truth (as Clavius believed it did), and the other nothing but error, the adherents of error could still refuse to accept the truth. But mathematics was different: with mathematics, the truth forces itself upon its audience whether they like it or not. One could dispute the Catholic doctrine of the sacraments, but one could not deny the Pythagorean theorem; and no one could challenge the correctness of the new calendar, based as it was on detailed mathematical calculations. Here, Clavius believed, was a key to the ultimate triumph of the Church.

Kokios matematikos reikėjo jėzuitams? Tokios, kokia buvo to meto geometrija atėjusi iš antikos laikų. Eukleideso Pradmenų variante Claviusas įterpė ,,Įvadinį esė apie matematikos dalyką“ (In disciplinas mathematicas prolegomena), kuriame jis žavisi geometrijos teiginių įrodymų tikrumu (angl. certainty of demonstrations). Alexanderio teigimu, tai yra aistringas kreipimasis agituojant už matematikos galios ir jos viršenybės kitoms intelektinės veiklos sritims pripažinimą. Alexanderis cituoja Claviusą (64 pusl):

„The theorems of Euclid,“ he continues, „and the rest of the mathematicians, still today as for many years past, retain in the schools their true purity, their real certitude, and their strong and firm demonstrations … And thus so much do the mathematical disciplines desire, esteem, and foster the truth that they reject not only whatever is false, but even anything merely probable, and they admit nothing that does not lend support and corroboration to the most certain demonstrations.“

Tokios matematikos plėtra Claviusui buvo planas, kuriuo turėjo eiti Jėzaus Draugija siekdama įtvirtinti katalikų tikėjimą. Claviuso planui įgyvendinti matematika turėjo tapti jėzuitų vykdomo švietimo programos ir pačių jėzuitų ruošimo pagrindine disciplina.  Alexanderis rašo [72 pusl.]:  

Clavius’s mathematical curriculum did not just teach the students specific competencies. More important, it demonstrated how absolute eternal truths shape the world and govern it.

1599 metais jėzuitų priimta švietimo programa Ratio studiorum atspindėjo Claviuso idėjas sausoje ir sutrumpintoje formoje, kaip ten pat teigia Alexanderis. Pavyzdžiui, kiekvienas moksleivis turėjo studijuoti  Eukleideso geometrijos pagrindus ir tie iš jų, kurie parodė matematinį talentą, buvo skatinami toliau jį vystyti. Be to, Clavius siekė įsteigti matematikos akademiją prie Collegio Romano ir jam tai pavyko. Jėzuitai sugebėjo pakelti to meto matematikos studijų lygį Europoje. Eukleideso geometrija buvo jėzuitų matematinio ugdymo branduolys.

This was not a stylistic choice, but a deaply held ideological commitment: the whole point of studying and teaching mathematics was that it demonstrated how universal truth imposed itself upon the world – rationally, hierarchically, and inescapably. Ideally, the Jesuits believed, the truth of religion would be imposed on the world just like geometrical theorems, leaving no room for avoidance or denial by Protestants or other heretics and leading to the inevitable triumph of the Church. For the Jesuits, mathematics must be studied according to the principles and procedures of Euclid, or it should not be studies at all. A mathematics that ran counter to these practices not only was useless to their purposes, but it would challenge their unconquerable faith that truth, handed down through the hierarchy of the universal Catholic Church, would inevitably prevail. [Alexander, 74 pusl.] 

Claviuso idėjos paliko stiprų pėdsaką tolesnėje jėzuitų matematinėje tradicijoje. Jėzaus Draugijos matematikai ribojo savo veiklą laiko išbandytais ir patikimais metodais.  Tarp kitko, šiais laikais veikia Claviuso grupe pasivadinę Claviuso pasekėjai, kurie populiarina teologijos ir matematikos ryšius.

Tuo pat metu, 17 amžiaus Europoje, atgimė kitokio pobūdžio matematinės idėjos. Jų autoriai naudojo aukščiau suformuluotą intuityvią prielaidą apie tiesės ir kitų geometrinių kūnų struktūrą. Kadangi Eukleideso geometrija tapo jėzuitų matematikos idealu ir Katalikų Bažnyčios autoriteto grąžinimo įrankiu, bet kokia kitokia matematika jėzuitams liko nepriimtina ir naikintina bet kuriomis priemonėmis. Todėl be galo mažų dydžių idėja tapo jėzuitų kritikos taikiniu ir politinės kovos objektu. Jėzuitai kovą laimėjo apie 1670-uosius metu, kada Italijoje neliko nei vieno matematiko savo tyrimuose naudojančio nedalomųjų metodą. Šios pergalės ir gal būt kitų susiklosčiusių aplinkybių pasekmė buvo kelis amžius trukęs Italijos išnykimas iš Europos kultūrinės veiklos žemėlapio.

 Galileo matematinis atomizmas

Iki jėzuitų pergalės italų matematikai Galileo Galilei, Bonaventura Cavalieri , Evangelista Torricelli ir kiti naudojo nedalomųjų metodą naujiems reiškiniams aiškinti ar naujiems faktams atrasti.  Archimedesas, panaudojęs šį metodą, stengėsi atrastą faktą pagrįsti kitais logiškai nepriekaištingais metodais, arba, teisingiau pasakius, tokiais metodais, kurie tuo metu buvo laikomi legaliais. Skirtingai nuo jo, italų matematikai nevengė metodo paradoksalumo. Priešingai, jie stengėsi atskleisti paradoksalumą ir naudoti jį aiškinantis matematinę esmę.

1621 metais Cavalieri savo laiške Galileo klausė jo nuomonės apie nedalomųjų metodą, dabar vadinamą Cavalieri principu. Cavalieri klausė Galileo: Ar leistina plokštumą tapatinti su visomis tos pačios krypties (lygiagrečiomis) tiesėmis? Klausimas yra to paties pobūdžio, kaip aukščiau suformuluota prielaida apie tiesės struktūrą. Galileo netiesiogiai atsakė į šį klausimą savo knygoje Discourses and Mathematical Demonstrations relating to Two New Sciences, kuri publikuota 1638 metais Olandijoje jau po autoriaus bendravimo su jėzuitų inkvizicija.  

 Knygos, toliau vadinamos Two New Sciences, turinys turi pokalbio formą. Pokalbyje dalyvauja Salviati (Galileo    atstovas), Simplicio (kritikas su Aristotelio pažiūromis) ir Sagredo (išmintingas tarpininkas). Vienas iš knygos epizodų  aiškina, kodėl tiesę sudaro be galo daug nedalomųjų tarp kurių yra tuščia erdvė. Galileo naudoja iš antikos laikų žinomą idėją, jog gamta vengia tuščios erdvės (horror vacui), tuo norėdamas paaiškinti, kas sieja medžiagą apsaugodamas ją nuo išsisklaidymo.  Pagal jį, bet kurią fizikinę medžiagą sudaro nedalomi atomai, kuriuos skiria tuščia erdvė. Šį aiškinimą jis perkėlė ir geometrinės tiesės struktūrai. 

 Be to, Galileo naudoja taip vadinamą Aristotelio ratų paradoksą (Aristotle’s wheel paradox):

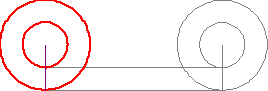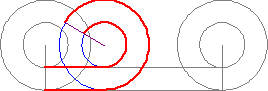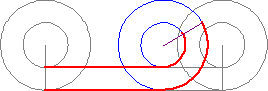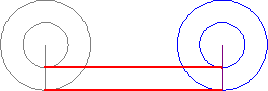
 Du sujungti skirtingo dydžio ratai juda, sudarydami iliuziją, kad jų apskritimų ilgiai sutampa. Iš tikro, gaunamos dvi raudonos atkarpos nurodo tik abipus vienareikšmę atitiktį tarp dviejų skirtingų apskritimų ilgių, bet ne jų sutapimą. Galileo papildo šios abipus vienareikšmės atitikties iliustraciją nagrinėdamas į apskritimus įbrėžtus daugiakampius. Toliau yra ištrauka iš Galileo knygos Two New Sciences [68-72 pusl.]:

SALVIATI. Now since we have arrived at paradoxes let us see if we cannot prove that within a finite extent it is possible to discover an infinite number of vacua. First it is necessary to consider a proposition, not treated by others, but upon which depends the solution of the problem and from which, if I mistake not, we shall derive other new and remarkable facts. For the sake of clearness let us draw an accurate figure.

 About G as a center describe an equiangular and equilateral polygon of any number of sides, say the hexagon ABCDEF. Similar to this and concentric with it, describe another smaller one which we shall call HIKLMN. Prolong the side AB, of the larger hexagon, indefinitely toward S; in like manner prolong the corresponding side HI of the smaller hexagon, in the same direction, so that the line HT is parallel to AS; and through the center draw the line GV parallel to the other two. This done, imagine the larger polygon to roll upon the line AS, carrying with it the smaller polygon. It is evident that, if the point B, the end of the side AB, remains fixed at the beginning of the rotation, the point A will rise and the point C will fall describing the arc CQ until the side BC coincides with the line BQ, equal to BC. But during this rotation the point I, on the smaller polygon, will rise above the line IT because IB is oblique to AS; and it will not again return to the line IT until the point C shall have reached the position Q. The point I, having described the arc IO above the line HT, will reach the position O at the same time the side IK assumes the position OP; but in the meantime the center G has traversed a path above GV and does not return to it until it has completed the arc GC. This step having been taken, the larger polygon has been brought to rest with its side BC coinciding with the line BQ while the side IK of the smaller polygon has been made to coincide with the line OP, having passed over the portion IO without touching it; also the center G will have reached the position C after having traversed all its course above the parallel line GV. And finally the entire figure will assume a position similar to the first, so that if we continue the rotation and come to the next step, the side DC of the larger polygon will coincide with the portion QX and the side KL of the smaller polygon, having first skipped the arc PY, will fall on YZ, while the center still keeping above the line GV will return to it at R after having jumped the interval CR. At the end of one complete rotation the larger polygon will have traced upon the line AS, without break, six lines together equal to its perimeter; the lesser polygon will likewise have imprinted six lines equal to its perimeter, but separated by the interposition of five arcs, whose chords represent the parts of HT not touched by the polygon: the center G never reaches the line GV except at six points. From this it is clear that the space traversed by the smaller polygon is almost equal to that traversed by the larger, that is, the line HT approximates the line AS, differing from it only by the length of one chord of one of these arcs, provided we understand the line HT to include the five skipped arcs.

 Now this exposition which I have given in the case of these hexagons must be understood to be applicable to all other polygons, whatever the number of sides, provided only they are similar, concentric, and rigidly connected, so that when the greater one rotates the lesser will also turn however small it may be. You must also understand that the lines described by these two are nearly equal provided we include in the space traversed by the smaller one the intervals which are not touched by any part of the perimeter of this smaller polygon.

Let a large polygon of, say, one thousand sides make one complete rotation and thus lay off a line equal to its perimeter; at the same time the small one will pass over an approximately equal distance, made up of a thousand small portions, each equal to one of its sides, but interrupted by a thousand spaces which, in contrast with the portions that coincide with the sides of the polygon, we may call empty. So far the matter is free from difficulty or doubt.

But now suppose that about any center, say A, we describe two concentric and rigidly connected circles; and suppose that from the points C and B, on their radii, there are drawn the tangents CE and BF and that through the center A the line AD is drawn parallel to them, then if the large circle makes one complete rotation along the line BF, equal not only to its circumference but also to the other two lines CE and AD, tell me what the smaller circle will do and also what the center will do. As to the center it will certainly traverse and touch the entire line AD while the circumference of the smaller circle will have measured off by its points of contact the entire line CE, just as was done by the above mentioned polygons. The only difference is that the line HT was not at every point in contact with the perimeter of the smaller polygon, but there were left untouched as many vacant spaces as there were spaces coinciding with the sides. But here in the case of the circles the circumference of the smaller one never leaves the line CE, so that no part of the latter is left untouched, nor is there ever a time when some point on the circle is not in contact with the straight line. How now can the smaller circle traverse a length greater than its circumference unless it go by jumps?

SAGREDO. It seems to me that one may say that just as the center of the circle, by itself, carried along the line AD is constantly in contact with it, although it is only a single point, so the points on the circumference of the smaller circle, carried along by the motion of the larger circle, would slide over some small parts of the line CE.

SALVIATI. There are two reasons why this cannot happen. First because there is no ground for thinking that one point of contact, such as that at C, rather than another, should slip over certain portions of the line CE. But if such slidings along CE did occur they would be infinite in number since the points of contact (being mere points) are infinite in number: an infinite number of finite slips will however make an infinitely long line, while as a matter of fact the line CE is finite. The other reason is that as the greater circle, in its rotation, changes its point of contact continuously the lesser circle must do the same because B is the only point from which a straight line can be drawn to A and pass through C. Accordingly the small circle must change its point of contact whenever the large one changes: no point of the small circle touches the straight line CE in more than one point. Not only so, but even in the rotation of the polygons there was no point on the perimeter of the smaller which coincided with more than one point on the line traversed by that perimeter; this is at once clear when you remember that the line IK is parallel to BC and that therefore IK will remain above IP until BC coincides with BQ, and that IK will not lie upon IP except at the very instant when BC occupies the position BQ; at this instant the entire line IK coincides with OP and immediately afterwards rises above it.

SAGREDO. This is a very intricate matter. I see no solution. Pray explain it to us.

SALVIATI. Let us return to the consideration of the above mentioned polygons whose behavior we already understand. Now in the case of polygons with 100000 sides, the line traversed by the perimeter of the greater, i. e., the line laid down by its 100000 sides one after another, is equal to the line traced out by the 100000 sides of the smaller, provided we include the 100000 vacant spaces interspersed. So in the case of the circles, polygons having an infinitude of sides, the line traversed by the continuously distributed [cantinuamente disposti] infinitude of sides is in the greater circle equal to the line laid down by the infinitude of sides in the smaller circle but with the exception that these latter alternate with empty spaces; and since the sides are not finite in number, but infinite, so also are the intervening empty spaces not finite but infinite. The line traversed by the larger circle consists then of an infinite number of points which completely fill it; while that which is traced by the smaller circle consists of an infinite number of points which leave empty spaces and only partly fill the line. And here I wish you to observe that after dividing and resolving a line into a finite number of parts, that is, into a number which can be counted. It is not possible to arrange them again into a greater length than that which they occupied when they formed a continuum and were connected without the interposition of as many empty spaces. But if we consider the line resolved into an infinite number of infinitely small and indivisible parts, we shall be able to conceive the line extended indefinitely by the interposition, not of a finite, but of an infinite number of infinitely small indivisible empty spaces.

Šio samprotavimo išvada – geometrinę tiesę sudaro be galo daug nedalomų taškų, kuriuos skiria labai maži tuščios erdvės tarpai. Galileo išvada netenkino jėzuitų. Jėzuitams imponavo toks matematinis samprotavimais, kuris grindžiamas akivaizdžiomis prielaidomis ir aiškia logine dedukcija. Matematikos išvados jėzuitų požiūriu, yra aukščiau realios tikrovės reiškinių. Galileo šią tvarką apvertė aukštyn kojomis. Pagal jį, intuityvus tikrovės supratimas perkeliamas į matematiką.

Cavalieri ir Torricelli požiūriai į matematiką iš esmės sutapo su Galileo požiūriu. Alexanderio knyga tai akivaizdžiai parodo. Italų matematikų idėjas perėmė kitų šalių matematikai. Tarp jų Pierre de Fermat  Prancūzijoje,  Johnas Wallisas ir Isaacas Barrow Anglijoje. Kitos kartos matematikai nedalomųjų metodą keitė  Isaaco  Newtono fliuksijų metodu bei Gottfrido Leibnizo diferencialiniu ir integraliniu skaičiavimu. Tuo tarpu Italijoje padėtis šiuo atžvilgiu pasikeitė [Alexander, 117 pusl.]:

In their own land, however, Galileo, Cavalieri, and Torricelli would have no successors. For just as Italian mathematics was being deprived of the leadership of Galileo and his disciples, the tide in Italy was turning decisively against their brand of mathematics. The Society of Jesus, which had long viewed the method of indivisibles with suspicion, had swung into action. In a fierce decades-long campaign, the Jesuits worked relentlessly to discredit the doctrine of the infinitely small and deprive its adherents of standing and voice in the mathematical community. Their efforts were not in vain: as 1647 [Torricelli mirties metai-R.N.] was drawing to a close, the briliant tradition of Italian mathematics was coming to an end as well. It would be centuries before the land of Galileo, Cavalieri, and Torricelli was once again home to creative mathematicians of the highest rank.

Italijos matematika buvo ne vienintelis jėzuitų veiklos rezultatas. Konkreti matematinė idėja buvo pretekstu kovai dėl tokių klausimų kaip absoliuti valdžia ir tiesa. Jėzuitai buvo įsitikinę, kad tiesa yra viena, o Eukleideso geometrija yra pavyzdys sistemos, kurioje tokia tiesa rodo savo absoliutumą. Galileo ir jo bendraminčiai taip pat ieškojo tiesos, bet ėjo priešingu keliu. Vietoje tiesos primetimo pasauliui, jie studijavo pasaulį tam, kad rasti tiesą. Politinėje plotmėje šis skirtumas reiškė pasirinkimą tarp totalitarizmo ir liberaliosios demokratijos. Visa tai vyko šiuolaikinės pasaulio tvarkos atsiradimo aušroje, 17-ame amžiuje. Alexanderio knygoje yra daugybė tokios kovos konkrečių pavyzdžių.  

Kiti man žinomi tekstai ta pačia tema:

• R. Feldhay. The use and abuse of mathematical entities: Galileo and the jesuits revisited. In: P. Machamer (Ed.) The Cambridge Companion to Galileo. 1998.
• The Jesuits: Pioneers of Mathematics as University Subject. Beastrabban’s Weblog

Pastabos. Jėzuitų veikla Lietuvoje

Jėzaus Draugijos kova su protestantizmu bei jos švietėjiška veikla pasiekė ir mūsų kraštus. Jėzuitų uolumas sustabdė protestantizmo plėtrą pietų Vokietijoje, Lenkijoje ir Lietuvoje.  Apie jėzuitų veiklą Lenkijoje Alexanderio knygoje rašoma:

Much like Germany, sixteenth-century Poland seemed well on its way to accepting one form or another of Protestantism when Catholic noblemen invited Jesuits to open their colleges there in the 1560s. They soon gained the trust support of the Polish royal family, which helped the Jesuits expand from five colleges in 1576 to thirty-two colleges by 1648. The Jesuits became the educators of the Polish ruling class, both the rural aristocracy and the urban elite, while in Rome they educated a devoted cadre of priests who returned to Poland to take up the leadership of the Church. So close were the Jesuits to the Polish monarchs, that King Sigismund III (1587-1632) [Zigmantas Vaza – R.N.] was known as the „Jesuit King“ and his son Jan II Kazimierz (1648-68) [Jonas Kazimieras Vaza – R.N.] was a member of the order and a cardinal before assuming the throne. Poland was transformed: a nation that had previously prided itself on religious tolerance, and had opened its churches and parishes to the reformers, became the devout Catholic land we still recognize today. In Poland as elsewhere, the Jesuit intervention proved decisive. [cit. iš A. Alexander. Infinitesimal. 47 pusl.]

Apie Jėzaus Draugijos veiklą Lietuvoje, apie jėzuitų švietimo sistemą ir matematiką mūsų krašte turime ne vieną knygą ar straipsnį.   Pavyzdžiui,

• B. Riaubos ir N. Vasiliauskaitės knyga ,,Senojo Vilniaus universiteto matematikos istorija“, 2012.
• interviu su R. Šviedriu. Modernusis mokslas ir jėzuitai (6). Mokslo Lietuva, 2007, Nr 1.
• Vilniaus universiteto bibliotekos interneto svetainė. Cituoju: ,,…pasak jėzuitų provincijolo Pranciškaus Sunyerio (Franciscus Sunyer, Sunner, 1532–1580), – mokyti filosofijos be matematikos – tas pats, kaip rėčiu semti vandenį.“
• Kita skaičiavimo metodų istorijos pusė. Interneto svetainė vartiklis.lt 
• G. Vitkus. Jėzuitų reikšmė Lietuvos švietimui XVI-XVIII a. Interneto svetainė bernardinai.lt 2011-05-16. Cituoju: ,,Apžvelgiant jėzuitų švietimą nuo pirmosios kolegijos Vilniuje atidarymo 1569 m. iki popiežiaus Klemenso XIV bulės, panaikinusios Jėzaus Draugijos veiklą, paskelbimo Vilniaus jėzuitų akademijoje 1773 m., reikia pripažinti, kad jėzuitai ištisus 200 metų buvo patys veikliausi ir pagrindiniai Lietuvos švietėjai.“ 
• I. Urbonaitė. Vilniaus Jėzuitų gimnazija mini 440 gimtadienį. DELFI, 2010 kovo 3 d. „Kalbėdami su istorikais, ginčijomės, ar galima Vilniaus jėzuitų kolegijos steigimą vadinti gimnazijos pradžia, tačiau manome, kad galima“, – DELFI sakė mokyklos direktorius Virgilijus Saulius SJ.
  
• I. Urbonaitė-Vainienė. Mokykla nesutalpina norinčių: atskyrė berniukus, ketvirtadienį padarė laisvą. DELFI, 2016 sausio 9 d.

Bet šie darbai skirti iš esmės asmenybių ir įvykių istorijai. Matematikos idėjų evoliucijos aptarimo ten nėra. Bent jau aš nežinau. Gaila, nes gyvendami tik šia diena bei nesirūpindami savo ir pasaulio kultūros pažinimu, plaukiame gyvenimo paviršiumi.