Skaičių ir dydžių daugybos apibrėžtis

Matematika Add comments

Grd 062020

Šiame įraše apžvelgiama pamiršta ir vėl atsimenama geometrinė daugybos konstrukcija, kurios pradininku yra René Descartesas. Daugyba yra proporcijos sąvokos variantas. Pagal ją, vienetas yra daugikliui tas pats, kas dauginamasis yra sandaugai. Ši daugyba vadinama įvairiai: daugybos prigimtimi; daugybos esme; daugyba kaip vieneto keitimas (angl. multiplication as a change in units); arba daugyba kaip mastelio keitimas (angl. multiplication as scaling). Mokyklinėje matematikoje populiari, kartotine sudėtimi vadinama, daugyba yra apžvelgiamos daugybos atskiras atvejis.

Daugybos veiksmo konstruktyvi apibrėžtis įdomi visų pirma pedagoginiu požiūriu. Natūraliųjų skaičių aibėje atliekama daugyba paprastai vadinama kartotine sudėtimi. Taip ji suprantama ne tik pradinėse klasėse bet ir vėliau, kai pasitelkiama rekursija Peano aksiomų kontekste. Aukštojoje mokykloje dažnai apsiribojama supažindinimu su realiųjų skaičių lauko struktūros aksiomomis.

Įdomi ne tik konstruktyvi daugybos apibrėžtis. Kartu su apibrėžtimi svarbu suprasti kaip jos pagalba gaunamos įprastinės daugybos veiksmo savybės. Pavyzdžiui, būtų gerai turėti realiųjų skaičių aibėje konstruktyviai apibrėžtą sandaugą, kurios atskiru atveju yra lygybė (-1)(-1)=1. Galiausiai daugybos apibrėžties klausimas yra įdomus matematikos idėjų istorijos kontekste.

Ši apžvalga pagrįsta įvairiais šaltiniais. Nėra vieno straipsnio, kuriame būtų paminėti bent dauguma šios srities darbų. Šaltiniuose nagrinėjami daugybos kontekstai yra labai įvairūs. Todėl apibrėžiant daugybą turime didelę tos pačios idėjos interpretacijų įvairovę. Ši apžvalga yra bandymas jas suprasti. Apžvalga buvo pristatyta Matematikos mokymo seminare 2020 m. balandžio 30 d.

Daugyba pagal Descartesą

Šiais laikais Descarteso sandauga dažniausiai vadinama dviejų aibių sandauga lygi tų aibių elementų sutvarkytų porų aibei. Kai dauginamos aibės yra realiųjų skaičių intervalai, tai gauto stačiakampio ploto pagalba galima apibrėžti realiųjų skaičių sandaugą. Tačiau šis skyrelis apie kitokią geometrinę sandaugos konstrukciją. Tą, kurią René Descarte (1596 kovo 31 – 1650 vasario 11.) iš tikro pasiūlė savo knygos Discourse de la methode (1637) priede La Gèomètrie. Apie daugybą pagal Descartesą rašome remdamiesi australų matematikos istoriko Jonathan J. Crabtree darbu (2017).

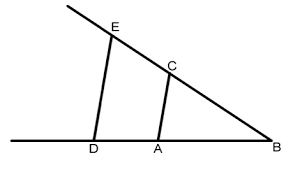
1 piešinys. Daugyba pagal Descartesą.

1 apibrėžtis. Šiame piešinyje tarkime, kad atkarpa BA yra vienetas. Tarkime, kad dauginame atkarpas BD ir BC. Sujungę taškus A ir C, brėžiame atkarpą DE lygiagrečią atkarpai AC. Atkarpa BE yra ieškoma atkarpų BD ir BC sandauga.

Jei reikia dalinti BE iš BD, tai jungiame taškus E ir D, po to brėžiame AC lygiagrečią DE. Atkarpa BC yra dalybos rezultatas.

Panašiu geometriniu būdu Descartesas apibrėžė ir kvadratinę šaknį. Šios aritmetinės operacijos toliau naudojamos geometriškai spręsti kvadratines lygtis. Atitinkamas sprendinių formules išreikšdamas geometriškai.

Daugybos ir dalybos pagal Descartesą apibrėžtyse slypi proporcijos idėja kartu su naujo nario – vieneto – įtraukimu į daugybos procesą. Daugyba pagal Descartesą suformuluota žodžiais skamba taip: kaip vienetas susijęs su daugikliu, taip dauginamasis susijęs su sandauga.

Pagal Euklido Pradmenis skaičius yra vienetų daugis (angl. multitude of units), ir vienetas nėra skaičius. Crabtree teigimu skaičių 1 atkarpai priskyrė Leonardo Pisano 1220 m. savo Praktinėje Geometrijoje. Nei prieš jį nei keletą šimtmečių po jo, vienetas nebuvo laikomas skaičiumi (vakarų matematinėje kultūroje).
Tik 16 amžiuje Pisano idėją vėl panaudojo Van Ceulenas. Descartesas rašydamas apie vienetą pamini tik Euklidą.

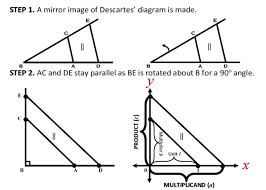
Akivaizdu, kad kampo B didumas 1 piešinyje nėra svarbus. Todėl jį galima pakeisti stačiuoju, visą piešinį pasukti ir patalpinti plokštumoje su koordinačių sistema kaip 2 piešinyje.

2 piešinys. Kita daugybos pagal Descartesą forma (Crabtree, 2017).

Gert Schubringo (2005, 49 pusl.) teigimu, nors Descartesas naudojo neigiamus skaičius, bet juos traktavo kaip nelygiaverčius teigiamiesiems skaičiams. Jo darbuose visi grafikai nupiešti koordinačių plokštumos pirmąjame ketvirtyje. Nei Descarteso plokštuma, nei anksčiau minėta Descarteso sandauga
nėra susijusios su René Descartesu ir jo geometrine daugybos konstrukcija.

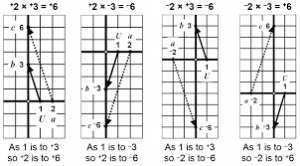
1707 m. Isaac Newtonas parašė Arithmetica Universalis. Joje daugyba apibrėžta Descarteso būdu naudojant beveik tą patį brėžinį. Bet jis nuėjo toliau daugybą pratęsdamas neigiamiems skaičiams ir grafikus brėžė visuose koordinačių plokštumos ketvirčiuose. Kaip tai veikia galima pamatyti
3 piešinyje dauginant $\pm 2$ iš $\pm 3$ .

3 piešinys. Teigiamų ir neigiamų skaičių daugyba pagal Descartesą (Crabtree, 2017).

Daugyba atkarpų aritmetikoje

Pradėsiu atkarpų kongruencijos ekvivalentumo klasių daugyba. Šios klasės yra aibės, ne skaičiai; jos vadinamos atkarpų ilgiais. Taip daroma sekant senovės graikų matematikos tradicijomis. Kalbant trumpai vienai klasei priklauso visos tos atkarpos, kurios sutampa vieną uždėjus ant kitos. Taigi, konkreti atkarpa yra kurios nors ekvivalentumo klasės elementas. Daugybos veiksmas apibrėžiamas ekvivalentumo klasių aibėje.

Piešinys vaizduoja trikampius sudarytus iš konkrečių atkarpų. Pavyzdžiui, atkarpa BC priklauso ekvivalentumo klasei a. Panašiai yra ir su kampais. Kaip ir atkarpa, konkretus kampas yra aibė. Kampas CAB priklauso kongruencijos santykiu apibrėžtai ekvivalentumo klasei $\alpha$ .

4 piešinys. Atkarpų daugyba.

Atkarpų sandauga apibrėžta Davido Hilberto knygoje (1902, 15§). Čia Roberto Hartshorne knygoje (2000, 170 pusl.) kontekstas, kuriame apibrėžiama atkarpų daugyba yra Hilberto plokštuma. Daugiau apie ją yra šio teksto paskutiniame skyrelyje, o tiksliau yra 13 apibrėžtyje.

2 apibrėžtis. Hilberto plokštumoje su lygiagretumo aksioma (P) bet kurioms dviems atkarpų kongruencijos ekvivalentumo klasėms a, b jų \emph{sandauga} ab apibrėžiama taip. Pirma, brėžiame statųjį trikampį ABC su kraštinėmis $AB\in 1$ ir $BC\in a$ , o stačiojo kampo viršūnė yra B. Tegul $\alpha$ yra kampas ∠ BAC. Antra, brėžiame kitą statųjį trikampį DEF su kraštine $DE\in b$ ir kampu $\alpha$ prie viršūnės D. Tada ab yra ta atkarpų kongruencijos ekvivalentumo klasė, kuriai priklauso antrojo trikampio kraštinė EF.

Kita teorema įrodyta Hartshorne knygoje (2000, Proposition 19.1, 168 p.).

Teorema. Bet kurioje Hilberto plokštumoje su aksioma (P), atkarpų klasių sandaugai teisingi teiginiai:

$ab$ apibrėžta korektiškai visiems $a,b$ ;
$a{\cdot}1=a$ visiems $a$ ;
$ab=ba$ visiems $a,b$ ;
$a(bc)=(ab)c$ visiems $a,b,c$ ;
kiekvienam $a$ egzistuoja vienintelis $b$ toks, kad $ab=1$ ;
$a(b+c)=ab+ac$ visiems $a,b,c$ .

Įrodymas. 1. Tegul $a,b$ yra dvi atkarpų kongruencijos ekvivalentumo klasės ir tegul sandauga $ab$ sukonstruota pagal 2 apibrėžtį. Tegul A’B’C’ yra kitas statusis trikampis, kurio statinių ilgiai yra $1,a$ ir stačiojo kampo viršūnė yra B’. Pagal (C6) aksiomą arba pagal (SAS), A’B’C’ yra kongruentus trikampiui ABC. Gauname kongruentų kampą $\alpha$ . Jei D’E’F’ yra kitas statusis trikampis su kampu $\alpha$ ir kraštine $b$ , tai jis yra kongruentus trikampiui DEF pagal (ASA). Gavome kongruenčią atkarpą $E'F'\in ab$ .

Daugyba pagal McLoughlin ir Droujkova

Šiame skyrelyje realiųjų skaičių daugyba apibrėžiama geometriškai.

Peter F. McLoughlin ir Maria Droujkova (2013) teigimu matematikos mokytojai Amerikoje dažnai baigia universitetą niekada nematę šių dalykų:

Logiškai nepriekaištingo realiųjų skaičių daugybos apibrėžimo;
Įrodymo, kad du trikampiai turi lygius atitinkamus kampus tada ir tik tada, kai jų atitinkamų kraštinių ilgiai yra proporcingi;
Sąryšio tarp stačiakampio ploto ir skaičių sandaugos įrodymo.

Iš dalies to priežastimi yra mokyklinės matematikos kursas, kuriame daugybos, stačiakampio ploto ir trikampių panašumo apibrėžimai yra priklausomi vienas nuo kito.

3 apibrėžtis. Tegul $a$ ir $b$ yra realieji skaičiai. Descarteso plokštumos y- ir x-ašyse atidėkime taškus $a$ ir $b$ , atitinkamai. Sandauga $ab$ yra x-ų ašies sankirta su tiese, kuri yra lygiagreti atkarpai $\overline{(b,0),(0,1)}$ ir eina per tašką $(0,a)$ .

Ši geometrinė daugybos apibrėžtis apibendrina daugybą kaip kartotinę sumą.

2 teorema. Jei $a\not =0$ yra sveikasis skaičius ir $b$ bet kuris realusis skaičius, tai $ab=\sum_{i=1}^ab$ .

3 teorema. Bet kuriems realiesiems skaičiams $a$ ir $b$ teisinga:

$(-a)(-b)=ab$ ;
$a(-b)=(-a)b=-(ab)$ .

4 teorema. Jei $a\not =0$ yra realusis skaičius, tai egzistuoja vienintelis realusis skaičius $b\not =0$ toks, kad $ab = 1$ . Be to, $b$ vadinamas atvirkštiniu skaičiui $a$ ir žymimas $\frac{1}{a}$ .

Šiai daugybai teisingi komutatyvumo, asociatyvumo ir distributyvumo dėsniai.

5 teorema. Realiesiems skaičiams $a,c,b\not =0$ ir $d\not =0$ teisinga

$\frac{a}{b}{\cdot}\frac{c}{d}=\frac{a{\cdot}c}{b{\cdot}d}.$

4 apibrėžtis. Du trikampiai vadinami panašiais, jei atitinkami kampai yra lygūs.

6 teorema. Tegul trikampio $\triangle ABC$ kraštinės lygios skaičiams $a\leq b\leq c$ ir tegul trikampio $\triangle A_1B_1C_1$ kraštinės lygios skaičiams $a_1\leq b_1\leq c_1$ . Trikampiai $\triangle ABC$ ir $\triangle A_1B_1C_1$ yra panašūs tada ir tik tada kai egzistuoja skaičius $k>0$ toks, kad

$a=ka_1,\quad b=kb_1\quad\mbox{ir}\quad c=kc_1$ .

P. Katiliaus vadovėlyje (1966, 1 apibrėžimas, 193 pusl.) du trikampiai kongruentūs, jei atitinkami kampai yra kongruentūs ir atitinkamos kraštinės yra kongruenčios.

Lietuvos jaunųjų matematikų mokyklos metodinėje medžiagoje rašoma: ,,Du trikampiai vadinami panašiais, jeigu jų atitinkami kampai lygūs ir vieno trikampio kraštinės proporcingos atitinkamoms kito trikampio kraštinėms.“

Alternatyvi skaičių daugybos apibrėžtis:

5 piešinys. Iš interneto platybių (anonimas).

Dydžių daugyba

5 apibrėžtis. Sandauga $C$ yra susijusi su dauginamuoju $B$ taip, kaip daugiklis $A$ yra susijęs su vienetu.

Tarkime $A$ ir $B$ yra tos pačios rūšies dydžiai, t.y. jie yra pamatuojami tuo pačiu vienetu $V$ . Pavyzdžiui, $A$ ir $B$ yra atkarpos, kurių ilgiai metrais yra $a$ ir $b$ . Tokiu atveju apibrėžtas dydžių $A$ ir $B$ santykis $A:B$ išreiškiamas skaičiumi

$A:B=\frac{a}{b}.$

Tada dydžio $C$ skaitinė reikšmė $c$ turi savybę

$a=\frac{A}{V}=\frac{C}{B}=\frac{c}{b}$ .

Gauname, kad $A$ ir $B$ sandauga $C$ yra dydis įgyjantis reikšmę $c=ab$ atžvilgiu vieneto $V$ . Pavyzdžiui, daugindami metrus iš metrų gauname vėl metrus. Tuo tarpu naudojant sandaugos apibrėžimą kaip stačiakampio plotą, metras padaugintas iš metro duoda kvadratinį metrą (SIC).

Daugyba kaip vieneto keitimas

6 apibrėžtis. Tarkime, kad žinoma taisyklė pagal kurią skaičius yra susietas su vienetu. Tegul $a$ ir $b$ yra skaičiai. Skaičius $c$ vadinamas sandauga, jei vienetas yra daugikliui $a$ tas pats, kas dauginamasis $b$ yra skaičiui $c$ .
Skaičių $a$ ir $b$ sandaugą žymėsime $a\diamond b:=c$ , o daugybos veiksmą vadinsime vieneto keitimu.

Įprastinė realiųjų skaičių sandauga apibrėžiama algebrinio lauko aksiomų sistema tenkina šį apibrėžimą. Tuo galima įsitikinti skaičius siejant jų santykiu. Tegul $a{\cdot}b$ žymi įprastinę realiųjų skaičių $a$ ir $b$ sandaugą, t.y. ji tenkina algebrinio lauko aksiomas. Naudodami vieną iš daugelio realiųjų skaičių santykio išraišką, gauname

$\frac{a{\cdot}b}{b}=(a{\cdot}b){\cdot}b^{-1}=a{\cdot}(b{\cdot}b^{-1})=a{\cdot}1=\frac{a}{1}.$

Taigi, daugiklis $a$ yra susijęs su $1$ taip, kaip sandauga latex]a{\cdot}b[/latex] susijusi su dauginamuoju $b$ .

6 apibrėžtis naudinga apskaičiuoti sandaugą tais atvejais, kai žinoma konkreti skaičiaus reikšmės radimo taisyklė pasirinkus vienetą. Toliau nagrinėjami du tokios taisyklės pavyzdžiai.

Kartotinė sudėtis. Viena skaičiaus reikšmės nustatymo taisykle galėtų būti visų natūralųjį skaičių sudarančių vienetų suma. Pavyzdžiui, natūralusis skaičius $n$ išreiškiamas lygybe

$n = 1+\cdots+1,\quad n$ dėmenų. (1)

Ši lygybė nusako sąryšį tarp $n$ ir $1$ .

Tegul $m$ yra kitas natūralusis skaičius. Tolesni samprotavimai tinka, kai $m$ yra bet kuris realusis skaičius. Pagal 6 apibrėžimą, sandaugos $n\diamond m$ sąryšis su dauginamuoju $m$ yra toks pat kaip ir daugiklio $n$ sąryšis su vienetu $1$ . Laikydami $m$ nauju vienetu ir toliau taikydami skaičiavimo taisyklę (1), gauname lygybę

$n\diamond m = m+\cdots+m,\quad n$ dėmenų. (2)

Dešinėje (2) lygybės pusėje esantis reiškinys paprastai vadinamas kartotine suma, kartotinės sudėties rezultatas. Joje yra $n-1$ sudėties veiksmas. Kai $n=1$ , kartotinė suma (2) turi vienintelį dėmenį $m$ .

Kairėje (2) lygybės pusėje esantis reiškinys gaunamas 6 apibrėžtimi nusakytu būdu. Šiame reiškinyje užkoduotas keturių skaičių, $1,n,m,n\diamond m$ , proporcijos sąryšis. Šio sąryšio nagrinėjimui galėtų pagelbėti skirtingos situacijos, mokyklinėje matematikoje paprastai išreiškiamos tekstiniais uždaviniais. Tokių (multiplikatyvių) situacijų įvairovės nagrinėjimas nėra šios apžvalgos tikslu.

Matematikos mokymo bendruomenėje vienu metu vyko karštos diskusijos dėl to ar daugyba mokykloje turėtų būti mokoma tik kaip kartotinė sudėtis (žr. Wikipedia). Kita vertus pastaruosius dešimtmečius vis daugėjo tyrimų susijusių su multiplikatyviuoju samprotavimu naudojamu sprendžiant tekstinius uždavinius.

Skaičius kaip taškas skaičių tiesėje. Kita skaičiaus reikšmės nustatymo taisyklė naudojasi skaičių tiesės idėja. Skaičių tiesė gaunama kai geometrinėje tiesėje pasirenkame nulį ir vienetą. Po šio pasirinkimo visi skaičiai randami skaičių tiesėje vienareikšmiškai. Skaičių vietos skaičių tiesėje radimas naudojant geometrijos priemones buvo nagrinėtas anksčiau. Čia nagrinėsime trupmeninių skaičių
daugybą naudodami jų vietos skaičių tiesėje radimo taisyklę.

Pradėkime trupmenomis, kurios yra natūraliaisiais skaičiais. 6 piežinys iliustruoja daugybą kai $a=3$ ir $b=2$ . Rausvi skaičiai rodo dauginamąjį $b=2$ pradinėje skaičių tiesėje su vienetu $1$ . Žalsvi skaičiai rodo skaičių tiesės dalį, kurioje nauju vienetu laikomas $1'=a=3$ . Sandauga 6 gaunama perskaičiavus $b=2$ pagal tą
pačią taisyklę naujoje skaičių tiesėje.

6 piešinys. Daugyba keičiant vienetą.

6 piešinys iliustruoja du skaičiavimo būdus. Greta jau aptartojo pagal 6 apibrėžimą čia yra ir geometrinis sandaugos skaičiavimas pagal \emph{Descartes}ą. Nenuostabu, kad abu jie duoda tą patį rezultatą.

Prisiminsime trupmenos apibrėžtį iš H.-H. Wu (2011, 183 pusl.). Ji suteikia taisyklę pagal kurią ant skaičių tiesės gauname paprastąja trupmena pažymėtą tašką.

7 apibrėžtis. Tegul $n$ ir $m$ teigiami natūralieji skaičiai. Dalinant intervalą $[0,1]$ į $n$ lygių dalių, po to apjungus nuo 0 pirmas gautas dalis į vieną intervalą, jo dešinysis galas yra trupmena $\frac{m}{n}.$

Tegul $\frac{m}{n}$ ir $\frac{k}{l}$ yra dvi trupmenos. Pagal 6 ir 7 apibrėžimus, šių trupmenų daugyba keičiant vienetą reiškia trupmenos $\frac{m}{n}$ vietos radimą skaičių tiesėje, kurioje naujasis vienetas užima trupmenos $\frac{k}{l}$ vietą. Sandauga $\frac{m}{n}\diamond\frac{k}{l}$ yra tas pats, kas H.-H. Wu knygoje
apibrėžiama sąvoka „ $\frac{m}{n}$ of $\frac{k}{l}$ “ (2011, Section 15.4). Būtent.

Definition (2011, p. 246). $\frac{m}{n}$ of a fraction $\frac{k}{l}$ means the length of $m$ concatenated parts when the segment $[0,\frac{k}{l}]$ is devided into $n$ parts of equal length.

Ši apibrėžtis gali būti svarbi kai reikia atitinkamą tekstinio uždavinio situaciją interpretuoti kaip daugybą.

7 teorema. Turint trupmenas $\frac{m}{n}$ ir $\frac{k}{l}$ ir jas dauginant vieneto keitimu teisinga lygybė

$\frac{m}{n}\diamond\frac{k}{l}=\frac{m\diamond k}{n\diamond l}.$

Įrodymas. Rasime trupmenos $\frac{m}{n}$ vietą naujoje vienetinėje atkarpoje $[0,\frac{k}{l}]$ . Kadangi šią atkarpą reikia dalinti į $n$ lygių dalių, trupmeną $\frac{k}{l}$ pakeičiame jai ekvivalenčia trupmena $\frac{n\diamond k}{n\diamond l}$ . Kadangi $n\diamond k$ yra $n$ dėmenų kartotinė suma
$k+\cdots +k$ , intervalą $[0,\frac{n\diamond k}{n\diamond l}]$ sudaro $n$ intervalo $[0,\frac{k}{n\diamond l}]$ kopijų. Apjungę $m$
tokių kopijų, gauto intervalo dešinysis galas yra taške $\frac{m\diamond k}{n\diamond l}$ , ką ir reikėjo įrodyti.

Pastaroji teorema arba tiesiogiai tikrinant galima įsitikinti, kad daugyba pagal Descartesą leidžia vizualizuoti trupmenų daugybos savybes.

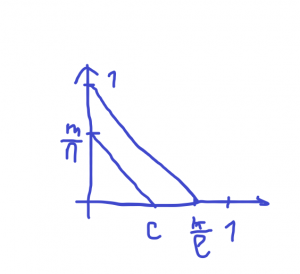
7 piešinyje matosi kaip pasirinkus trupmenas $\frac{k}{l}$ ir $\frac{m}{n}$ , po to sujungus taškus 1 su $\frac{k}{l}$ ir per tašką $\frac{m}{n}$ brėžiant lygiagrečią gauname tašką

$c=\frac{m}{n}\diamond\frac{k}{l}.$

7 piešinys. Trupmenų sandauga.

Man atrodo būtų gerai parengti mokymo priemonę ,,Trupmenų skaičiavimas geometrijos priemonėmis“, pradžiai mokytojams.

Istorinės pastabos. Matematikos istoriko Crabtree (2016) teigimu daugybos kaip vieneto keitimo idėja buvo prapuolusi šimtmečiams. Dar gerokai iki Descarteso (SIC), 1501 m. vokiečių matematikas Johann Huswirt apibrėžė daugybą taip:

[T]he creation of a number (product), being in proportion to a multiplicand, as the multiplier is to the unity.

Analogiškai dalyba:

Division is the creation of a quotient, being in proportion to a dividend, as the unit is to the divisor.

1677 m. anglas Edwardas Cockeris, knygos Cocker’s Arithmetick autorius, skyrių apie daugybą pradėjo žodžiais:

Multiplication is performed by two Numbers of like Kind for the Production of a Third, which will have such Reason (ratio) to the one, as the other hath to the Unit.

Pagal Crabtree (2016), Cockeris buvo vienas iš paskutiniųjų rašančių apie matematiką populiariai, kuris sandaugos prigimties formulavimą pateikė prieš pradėdamas jos praktinius skaičiavimus.

Panašiu metu apie daugybos prasmę ir jos geometrinę formą pagal Descartesą užsimenama prancūzų Antoine Arnauldo (1612-1694) ir Jean Presteto (1648-1691) matematikos vadovėliuose. Daugybos apibrėžties klausimas pasirodė svarbus kontraversijoje tarp abiejų prancūzų dėl ženklų sandaugos taisyklės. Kontraversija detaliai aprašyta Gert Schubring knygoje (2005, 2.5 Section). Įdomu, kad Arnauldas siūlė nenaudoti proporcijos neigiamiems skaičiams, nes lygybė $1:(-1)=(-1):1$ sukuria prieštarą: jei proporcijos pirmas narys yra didesnis už antrąjį, tai trečiasis narys taip pat turi būti didesnis už ketvirtąjį.

Hilberto plokštuma

Tiksliau – Hilberto aksiomomis pagrįsta plokštumos geometrija. Toliau suformuluotos pagrindinės aksiomas ir sąvokas paimtos iš Hartshorne (2000). Tai minimumas naudojamas apibrėžiant atkarpų daugybą. Daugumas faktų yra ir Katiliaus vadovėlyje(1966, III skyrius).

Taškai ir tiesės yra objektai, kurie yra apibrėžti netiksliai tokia prasme. Tariama, kad duota aibė, jos elementai vadinami taškais, o tam tikri poaibiai vadinami tiesėmis. Nėra pasakoma, kas yra taškais ir kokie poaibiai yra tiesėmis, bet reikalaujama, kad šios neapibrėžtos sąvokos tenkina aksiomas:

(I1) Bet kuriems dviems skirtingiems taškams A, B egzistuoja vienintelė juos turinti tiesė $\ell$ .

(I2) Kiekviena tiesė turi bent du taškus.

(I3) Egzistuoja trys nekolinearūs taškai (tai yra, trys taškai ne vis priklausantys vienai tiesei)

8 apibrėžtis. Incidencijos geometrija (priklausomumo geometrija) yra aibė, kurios taškais vadinami elementai ir tiesėmis vadinami poaibiai tenkina aksiomas (I1), (I2) ir (I3). Jei taškas P priklauso tiesei $\ell$ , tai sakoma, kad P yra ant $\ell$ arba $\ell$ eina per P.

Incidencijos geometrijos modeliu (pavyzdžiu) yra Descarteso plokštuma.

9 apibrėžtis. Dvi tiesės vadinamos lygiagrečiomis, jei jos neturi bendrų taškų. Kiekviena tiesė yra lygiagreti pati sau.

(P) (Lygiagretumo aksioma). Kiekvienam taškui A ir kiekvienai tiesei $\ell$ egzistuoja ne daugiau kaip viena tiesė einanti per A ir lygiagreti $\ell$ .

Sąryšis ,,tarp“ (betweenness) yra apibrėžtas netiksliai tokia prasme.

Tariama, kad trijų taškų A, B, C aibei galioja sąryšis ,,B yra tarp A ir C“. Reikalaujama, kad šiam sąryšiui teisingos keturios aksiomos.

(B1) Jei B yra tarp A ir C (rašoma A∗B∗C), tai A, B, C yra trys skirtingi taškai ant tiesės ir C∗B∗A.

(B2) Bet kuriems dviems skirtingiems taškams A, B egzistuoja toks taškas C, kad A∗B∗C.

(B3) Bet kuriems trims skirtingiems taškams ant tiesės, vienas ir tik vienas iš jų yra tarp kitų dviejų.

(B4) (Pašo aksioma). Tegul A, B, C yra trys nekolinearūs taškai ir tegul $\ell$ yra tiesė neinanti per kiekvieną iš jų. Jei tiesė $\ell$ eina per tašką D, esantį tarp A ir B, tai ji taip pat turi eiti per tašką esantį tarp A ir C arba turi eiti per tašką esantį tarp B ir C, bet ne per abu taškus.

10 apibrėžtis. Jei A ir B yra skirtingi taškai, tai atkarpa AB yra aibė taškų sudaryta iš taškų A, B ir visų taškų esančių tarp A ir B. Kitaip tariant, atkarpa yra aibė

$AB=\{A,B\}\cup\{C\colon\,A{\star}C{\star}B\}.$

Jei A, B, C yra nekolinearūs taškai, tai trijų atkarpų AB, BC, AC sąjunga yra trikampis. Taškai A, B, C yra trikampio viršūnės ir atkarpos AB, BC, AC yra trikampio kraštinės.

11 apibrėžtis. Turint du skirtingus taškus A, B, spindulys $\overrightarrow{AB}$ yra aibė sudarytas iš A ir visų tų taškų ant tiesės AB, kurie yra toje pačioje pusėje nuo A kaip ir B. Kitaip tariant, spindulys yra aibė

$\overrightarrow{AB}=AB\cup\{C\colon\,A{\star}B{\star}C\}.$

Tegul A, B, C yra trys taškai nesantys ant vienos tiesės. Kampas ∠BAC yra sąjunga dviejų spindulių $\overrightarrow{AB}$ ir $\overrightarrow{AC}$ , turinčių bendrą pradžią, vadinamą jo viršūne, ir nesančių ant tos pačios tiesės. (Taigi nėra ,,nulinio kampo“ ir nėra ,,tiesaus kampo“). Kitaip tariant, kampas yra aibė

∠BAC $=\overrightarrow{AB}\cup\overrightarrow{AC}.$

Kampo ∠BAC vidus yra sudarytas iš visų tokių taškų D, kad D ir C yra vienoje tiesės AB pusėje, o D ir B yra vienoje tiesės $AC$ pusėje. Jei ABC yra trikampis, tai jo vidus yra aibė taškų, kurie yra kiekvieno kampo ∠BAC, ∠ABC, ∠ACB vidaus taškais. (Hartshorne, 2000, 77 pusl.)

Dviejų atkarpų AB ir CD kongruencijos sąryšis, žymimas AB≅CD, apibrėžiamas netiksliai, t.y. reikalaujant tik aksiomų (C1), (C2), (C3) galiojimo.

8 piešinys. Atkarpų kongruencija.

(C1) Turint atkarpą AB ir turint spindulį r prasidedantį taške C egzistuoja vienintelis taškas D ant spindulio r toks, kad AB≅CD.

(C2) Jei AB≅CD ir AB≅EF, tai CD≅EF. Kiekviena atkarpa yra kongruenti sau pačiai.

(C3) Turint tris taškus A, B, C ant tiesės sąryšyje A∗B∗C ir turint tris kitus taškus D, E, F ant tiesės sąryšyje D∗E∗F, jei AB≅DE ir BC≅EF, tai AC≅DF.

8 teorema (Hartshorne, 2000, Proposition 8.1). Atkarpų aibėje kongruencija yra ekvivalentumo sąryšis.

12 apibrėžtis. Tarkime, kad turime dvi atkarpas AB ir CD. Pasirinkime AB galų tvarką (A,B). Tegul $\ell$ yra tiesė turinti taškus A, B ir tegul r yra spindulys tiesėje $\ell$ , kuriam priklauso B ir visi $\ell$ taškai esantys kitoje nuo B pusėje negu A. Tegul E yra vienintelis r taškas toks, kad CD≅BE. Tada atkarpa AE yra atkarpų AB ir CD suma priklausanti nuo tvarkos (A,B) ir žymima AE=AB+CD.

9 teorema (Sumos kongruencija). Tarkime, kad atkarpos AB≅A’B’ ir CD≅C’D’. Tada (AB+CD)≅(A’B’+C’D’).

Kadangi atkarpa AB yra lygi atkarpai BA, kongruencijos tikslumu atkarpų suma nepriklauso nuo tvarkos (A,B). Todėl atkarpų kongruencijos ekvivalentumo klasių aibėje suma apibrėžta korektiškai. Galima parodyti, kad kongruencijos tikslumu atkarpų suma yra komutatyvi ir asociatyvi.

Galiausiai kampų kongruencija apibrėžiama netiksliai ta prasme, kad reikalaujame tik aksiomų (C4), (C5), (C6) galiojimo.

(C4) Turint kampą ∠BAC ir turint spindulį $\overrightarrow{DF}$ , priešingose atkarpos DF pusėse egzistuoja kampai ∠EDF ir ∠FDG tokie, kad ∠BAC = ∠EDF = ∠FDG.

(C5) Turint bet kuriuos tris kampus $\alpha$ , $\beta$ , $\gamma$ , jei $\alpha{\cong}\beta$ ir $\alpha{\cong}\gamma$ , tai $\beta{\cong}\gamma$ . Kiekvienas kampas yra kongruentūs sau.

(C6) Turint kampus ABC ir DEF, tarkime, kad AB≅DE, AC≅DF ir ∠BAC ≅ ∠EDF. Tada du trikampiai yra kongruentūs, būtent, BC≅EF, ∠ ABC≅ ∠DEF ir ∠ACB ≅ ∠DEF.

Katiliaus vadovėlyje (192 pusl. apačioje) rašoma, kad Rozentalis (?) įrodė (C5) aksiomos nereikalingumą. Ši ir kitos vadovėlio pastabos nesuprantamos, nėra tikslių nuorodų.

10 teorema (Hartshorne, 2000, Proposition 9.1). Kampų aibėje kongruencija yra ekvivalentumo sąryšis.

13 apibrėžtis. Taškų aibė kartu su tiesėmis vadinamais poaibiais, bei neapibrėžtomis sąvokomis ,,tarp“ (betweenness), atkarpų kongruencija, kampų kongruencija vadinama Hilberto plokštuma, jei galioja aksiomos: (I1)-(I3), (B1-B4) ir (C1)-(C6).

Literatūra

Cocker, E. (1677). Cocker’s Arithmetic, p. 31. John Hawkins, London.
Crabtree, J. (2016). A new model of multiplication via Euclid. Vinculum, 53(2), 16.
Crabtree, J. (2017). Multiplication and division in the manner of René Descartes and Isaac Newton. In: Capital Maths. Proceedings of the 26th Biennial Conference of the Australian Association of Mathematics Teachers Inc., pp. 90-98.
Crippa, Davide. (2017). Descartes on the Unification of Arithmetic, Algebra and Geometry Via the Theory of Proportions. Revista Portuguesa de Filosofia T. 73, Fasc. 3/4, Ciências Formais e Filosofia: Lógica e Matemática / Formal Sciences and Philosophy: Logic and Mathematics, pp. 1239-1258.
Descartes, R. (1637). La Gèomètrie in Discourse de la Mèthode. I. Maire: [Holland] Leyde.
Descartes, R. Smith, D.E. \& Latham, M.L. (1925). The Geometry of Renè Descartes: With a Facsimile of the First Edition. Chicago: Open Court, 1925.
Hartshorne, R. (2000). Geometry: Euclid and Beyond. Springer.
Hilbert, D. (1902). The Foundations of Geometry. Engl. transl.
Huswirt, J. (1501). Enchiridion Algorismi, (Handbook of Algorithms) Cologne, Germany. (Multiplication definition translated by Ulrich Reich, Freie Universität, Berlin, Germany)
Katilius, P. (1966). Geometrijos pagrindai. Vilnius, Mintis.
Lietuvos jaunųjų matematikų mokyklos metodinė medžiaga ir užduotys. \url{https://www.mif.vu.lt/ljmm/kursb/ketv/ketvuzd.htm}
McLoughlin, Peter F., Droujkova, Maria. (2013). A Geometric Approach to Defining Multiplication. \url{https://arxiv.org/abs/1301.6602}
Schubring, Gert. (2005). Conflicts between Generalization, Rigor, and Intuition. Number Concepts Underlying the Development of Analysis in 17-19th Century France and Germany. Sources and Studies in the History of Mathematics and Physical Sciences. Springer.
Multiplication and repeated addition. Wikipedia.
Wu, Hung-Hsi. (2011). Understanding Numbers in Elementary School Mathematics. AMS.

Matematika kaip kultūros reiškinys

Skaičių ir dydžių daugybos apibrėžtis

Leave a Reply Cancel reply